Уроки по OpenGL с сайта OGLDev - Урок 31 - Тесселяция PN треугольников

Урок 31 - Тесселяция PN треугольников

В предыдущем уроке мы познакомились с Тесселяцией в OpenGL 4.x (этот урок сильно полагается на материал предыдущего, поэтому убедитесь, что вы знакомы с ним). Мы включили все соответствующие этапы и изучили, как делится наш меш, и сместили вершины, созданные процессом тесселяции для того, что бы преобразовать пустую гладкую поверхность в сложный рельеф камня. Использование конвейера тесселяции было достаточно простым, однако. Оценка в TES была просто интерполированием вершин оригинального треугольника через барецентрические координаты, генерируемые PG. Так как результат интерполяции был в плоскости исходного треугольника, мы использовали смещение для того, что бы создать неровности на поверхности.

В Этом уроке мы изучим более сложный метод Тесселяции, известный как PN (Point-Normal) Triangles (Точки-Нормали треугольников). Этот метод был темой работы 2001 Vlachos et al, и был представлен на презентации GDC2011, где его назвали "Tessellation On Any Budget" (Тесселяция любого бюджета) John McDonald. Идея, показанная этими работами, в замещении каждого треугольника в исходном меше геометрической поверхностью, известной как Поверхность Безье для смягчения низко полигональных моделей.

Поверхность Безье была открыта Pierre Bezier в 1960s как способ объяснения кривизны корпусов автомобилей. В двух словах, Поверхность Безье - полиномиальная функция, которая объясняет сглаживание и непрерывность поверхностей, которые целиком заданы через набор контрольных точек (CP). Полином имеет специальный атрибут, в то время как перемещение CP дает больший эффект в окрестности этой CPs. Эффект уменьшается при удалении от CP. Вы можете представить это как очень тонкую и гибкую ткань лежащую на полу. Если вы начнете поднимать ее в некоторой точке, то кривая, создаваемая тканью, будет все менее и менее изменяться при увеличении дистанции от этой точки (если бы ткань была бесконечно гибкой, мы бы, возможно, и не заметили эффекта нигде, кроме этой точки).

Полином поверхности Безье определен на единичном квадрате. То есть, подключая в функцию различные комбинаций из двух чисел в диапазоне [0-1], мы получим точку в 3D пространстве, которая точно принадлежит гладкой поверхности, описанной многочленом. Если вы добавите множество пар чисел в единичный квадрат и отобразите результат на экран, то в конечном итоге вы получить хорошее приближение поверхности.

Мы собираемся использовать частный случай поверхности Безье, называемый Треугольник Безье (Bezier Triangle), который имеет следующую формулу:

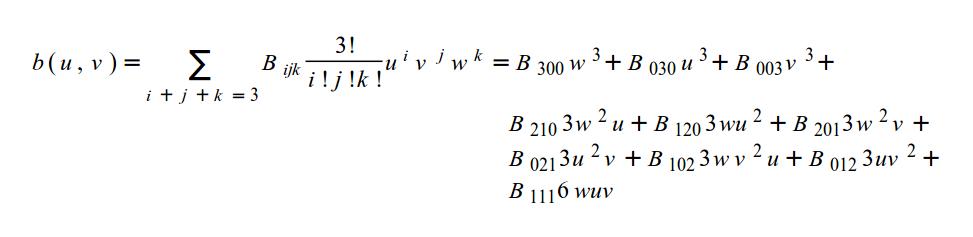
Давайте пройдем по ней шаг за шагом. 'u/v/w' - барецентрические координаты (т.е. всегда справедливо выражение 'u + v + w = 1'). Десять 'B_xyz' - CPs. Мы собираемся немного отклониться от классического определения Треугольника Безье и разместить CPs вот так:

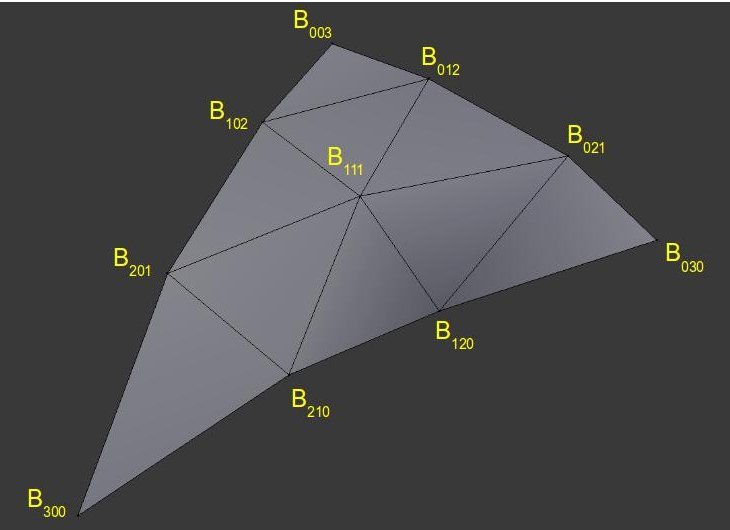
Как вы можете заметить, общая форма CPs напоминает немного пухлые поверхности поверх треугольника. Оценивая большое количество барецентрических координат в полиноме выше мы можем получить приблизительную поверхность в 3D пространстве.

Давайте посмотрим, как объединить эти математические понятия в конвейере тесселяции. Мы собираемся начать с треугольника, и это будет нашим входящем патчем (как и в предыдущем уроке). Мы создадим 10 CPs и определим TLs в TCS. PG будет разбивать область треугольника согласно TLs и TES будет вызываться для каждой новой точки. TES будет включать барецентрические координаты из PG и 10 CPs из TCS в полином треугольника Безье, а результатом будут координаты на распухшей поверхности. А дальше как обычно.

Последний не рассмотренный момент - как же создать CPs. Алгоритм метода PN треугольники таков:

Исходные вершины треугольника остаются не именными (их имена B₀₀₃, B₀₃₀ и B₃₀₀).
2 точки посередине на каждой стороне - одна координата равна 1/3, а другая 2/3.
Каждая средняя точка проецируется на плоскость, созданную ближайшей вершиной и ее нормалью:

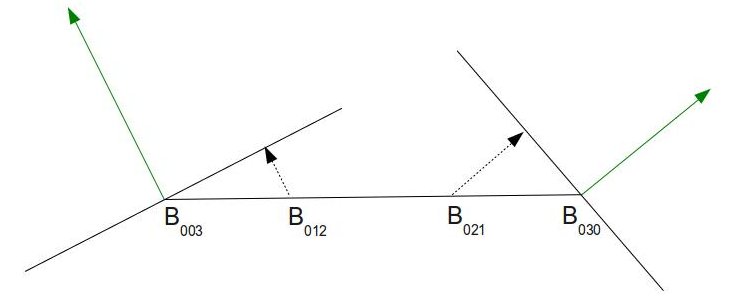
Изображение выше показывает треугольник сбоку. Каждая из 2-х крайних точек имеет свою нормаль (зеленая) из исходного меша. Комбинация точек и нормалей создает плоскость. Мы берем 2 точки посередине, которые нашли ранее, и проецируем их на плоскость ближайшей вершины (пунктирные линии).

Для того, что бы вычислить позицию B₁₁₁ мы берем вектор из центра исходного треугольника (среднее 3-х вершин) к среднему от 6 вершин посередине (после проецирования). Мы проходим вдоль вектора на половину его длины.

Смысл этой схемы очень прост. Когда вы имеете участок на меше, который довольно плоский, то это значит, что большинство вершинных нормалей будут направлены приблизительно в одном направлении, которое будет не слишком далеко от настоящей нормали треугольника. Это означает, что когда мы проецируем точки посередине на плоскость, они не сильно отодвинуться от поверхности треугольника. В результате мы получим "пухлость" в этой области. Но если область сильно крива, то тогда точки посередине будут двигаться дальше для избежания зазубрин в этой области. В демо вы можете увидеть, что мы используем низко полигональную модель Сюзанны, талисман Blender, которая состоит из около 500 полигона. Изломы силуэта очень хорошо заметны, особенно на голове. Проецируя средние точки по объяснению выше для создания CPs и используя тесселяцию для оценки треугольника Безье, мы создаем дополнительные CPs, которые дают дополнительную гладкость модели без затрат сил моделеров.

Литература:

Vlachos Alex, Jorg Peters, Chas Boyd and Jason L. Mitchell. "Curved PN Triangles". Proceedings of the 2001 Symposium interactive 3D graphics (2001): 159-66.
John McDonald. "Tessellation On Any Budget". Game Developers Conference, 2011.

Прямиком к коду!

lighting_technique.cpp:38

void main()
{
    WorldPos_CS_in = (gWorld * vec4(Position_VS_in, 1.0)).xyz;
    TexCoord_CS_in = TexCoord_VS_in;
    Normal_CS_in   = normalize((gWorld * vec4(Normal_VS_in, 0.0)).xyz);
}

VS получил только 1 изменение - нормаль должна быть нормирована после мировых преобразований. Причина в том, что TCS полагает, что нормаль единичной длины. В противном случае новые CPs будут созданы не корректно. Если мировые преобразования содержат изменения масштаба, то нормали не будут иметь единичную длину, поэтому мы их и нормируем.

lighting_technique.cpp:47

#version 410 core

// определяем количество CPs в выходящем патче
layout (vertices = 1) out;

    uniform float gTessellationLevel;

// атрибуты входящей CPs
in vec3 WorldPos_CS_in[];
in vec2 TexCoord_CS_in[];
in vec3 Normal_CS_in[];

struct OutputPatch
{
    vec3 WorldPos_B030;
    vec3 WorldPos_B021;
    vec3 WorldPos_B012;
    vec3 WorldPos_B003;
    vec3 WorldPos_B102;
    vec3 WorldPos_B201;
    vec3 WorldPos_B300;
    vec3 WorldPos_B210;
    vec3 WorldPos_B120;
    vec3 WorldPos_B111;
    vec3 Normal[3];
    vec2 TexCoord[3];
};

// атрибуты выходящей CPs
out patch OutputPatch oPatch;

Это начало TCS c небольшими изменениями. Первое на что требуется обратить внимание, это то, что мы выводим только 1 CP. Возможно вам это покажется странным, ведь идея PN треугольников в создании треугольника Безье с 10 CPs на поверхности треугольника. Итак почему же мы объявили единственную выходящую CP вместо 10? причина в том, что главная функция TCS будет вызвана столько раз, сколько определено выходящих CPs. В этом алгоритме мы должны рассматривать некоторые моменты иначе, что усложняет использование одной функции для всех точек. Вместо этого я инкапсулирую все данные выходящего патча в структуру OutputPatch выше и объявляю выходящую переменную, названную oPatch, этим типом. Главная функция TCS будет запускаться единожды для каждого патча и эта структура будет заполнена данными для всех 10 CPs. Реализация, которую представил McDonald на GDC 2011 (смотри литературу) предлагает версию, которая окажется более эффективной. В этой версии TCS вызывается 3 раза, что позволяет GPU распределить работу над одним патчем на 3 потока. В общем, если выходящие CPs были созданы используя этот алгоритм, то лучше (с точки зрения производительности) осуществлять этот алгоритм как есть в TCS и вызывать его для такого количества выходящих CPs, какое вам требуется.

Так же обратите внимание на то, что oPatch имеет префикс со встроенным ключевым словом patch. Это слово говорит, что данная переменная хранит содержимое патча, а не текущей выходящей CP. Компилятор может использовать это как рекомендацию для того, что бы удостоверится, что код, который будет обновлять эту переменную, будет запускаться один раз на патч вместо одно на CP (так как GPUs будет стараться обновить каждую выходящую CP в различном HW потоке).

Последнее изменение в этом участке - это позиция глаза в виде uniform-переменной была заменена уровнем тесселяции. Вместо установки TL согласно расстоянию от камеры (как в предыдущем уроке) мы позволим пользователю настроить ее используя кнопки '+' и '-'. Так будет проще наблюдать наблюдать различные эффекты в зависимости от изменения TL.

lighting_technique.cpp:122

void main()
{
    // Set the control points of the output patch
    for (int i = 0 ; i < 3 ; i++) {
        oPatch.Normal[i]   = Normal_CS_in[i];
        oPatch.TexCoord[i] = TexCoord_CS_in[i];
    }

    CalcPositions();

    // Calculate the tessellation levels
    gl_TessLevelOuter[0] = gTessellationLevel;
    gl_TessLevelOuter[1] = gTessellationLevel;
    gl_TessLevelOuter[2] = gTessellationLevel;
    gl_TessLevelInner[0] = gTessellationLevel;
}

Это главная функция TCS. 3 нормали и координаты текстуры копируются как есть из входного в выходящий патч. 10 CPs, которые мы хотим создать, хранят только значение позиции. Это происходит в соответствующей функции CalcPositions(), которая затем запускается. Наконец, TLs устанавливается в значение uniform-переменной.

lighting_technique.cpp:87

void CalcPositions(
{
    // Исходные вершины остаются без изменений
    oPatch.WorldPos_B030 = WorldPos_CS_in[0];
    oPatch.WorldPos_B003 = WorldPos_CS_in[1];
    oPatch.WorldPos_B300 = WorldPos_CS_in[2];

    // Стороны названы согласно противоположным вершинам
    vec3 EdgeB300 = oPatch.WorldPos_B003 - oPatch.WorldPos_B030;
    vec3 EdgeB030 = oPatch.WorldPos_B300 - oPatch.WorldPos_B003;
    vec3 EdgeB003 = oPatch.WorldPos_B030 - oPatch.WorldPos_B300;

    // Создание точек посередине каждой стороны
    oPatch.WorldPos_B021 = oPatch.WorldPos_B030 + EdgeB300 / 3.0;
    oPatch.WorldPos_B012 = oPatch.WorldPos_B030 + EdgeB300 * 2.0 / 3.0;
    oPatch.WorldPos_B102 = oPatch.WorldPos_B003 + EdgeB030 / 3.0;
    oPatch.WorldPos_B201 = oPatch.WorldPos_B003 + EdgeB030 * 2.0 / 3.0;
    oPatch.WorldPos_B210 = oPatch.WorldPos_B300 + EdgeB003 / 3.0;
    oPatch.WorldPos_B120 = oPatch.WorldPos_B300 + EdgeB003 * 2.0 / 3.0;

    // Проецируем каждую точку посередине на плоскость, определяемую ближайшей вершиной и ее нормалью
    oPatch.WorldPos_B021 = ProjectToPlane(oPatch.WorldPos_B021, oPatch.WorldPos_B030, oPatch.Normal[0]);
    oPatch.WorldPos_B012 = ProjectToPlane(oPatch.WorldPos_B012, oPatch.WorldPos_B003, oPatch.Normal[1]);
    oPatch.WorldPos_B102 = ProjectToPlane(oPatch.WorldPos_B102, oPatch.WorldPos_B003, oPatch.Normal[1]);
    oPatch.WorldPos_B201 = ProjectToPlane(oPatch.WorldPos_B201, oPatch.WorldPos_B300, oPatch.Normal[2]);
    oPatch.WorldPos_B210 = ProjectToPlane(oPatch.WorldPos_B210, oPatch.WorldPos_B300, oPatch.Normal[2]);
    oPatch.WorldPos_B120 = ProjectToPlane(oPatch.WorldPos_B120, oPatch.WorldPos_B030, oPatch.Normal[0]);

    // Находим центр
    vec3 Center = (oPatch.WorldPos_B003 + oPatch.WorldPos_B030 + oPatch.WorldPos_B300) / 3.0;
    oPatch.WorldPos_B111 = (oPatch.WorldPos_B021 + oPatch.WorldPos_B012 + oPatch.WorldPos_B102 +
        oPatch.WorldPos_B201 + oPatch.WorldPos_B210 + oPatch.WorldPos_B120) / 6.0;
    oPatch.WorldPos_B111 += (oPatch.WorldPos_B111 - Center) / 2.0;
}

Эта функция строит треугольник Безье на поверхности исходного треугольника согласно методу, объясненному в разделе теории. Имена соответствующих членов структуры OutputPatch аналогичны изображению выше для упрощения обзора. Логика очень проста и следует алгоритму шаг за шагом.

lighting_technique.cpp:78

vec3 ProjectToPlane(vec3 Point, vec3 PlanePoint, vec3 PlaneNormal)
{
    vec3 v = Point - PlanePoint;
    float Len = dot(v, PlaneNormal);
    vec3 d = Len * PlaneNormal;
    return (Point - d);
}

Эта функция используется в CalcPositions() для проецирования точек посередине на плоскость, определенную ближайшей вершиной и ее нормалью. Идея в том, что произведя скалярное произведение между нормалью и вектором 'v' из вершины до точки, которую мы хотим проецировать, мы получим длину проекции 'v' на нормали (она должна быть единичной длины). Это будет расстояние между точкой и ближайшей точкой на плоскости (то есть ее проекция). Мы умножаем длину на нормаль и вычитаем ее из точки для того, что бы получить проекцию. Следующее изображение иллюстрирует эти вычисления:

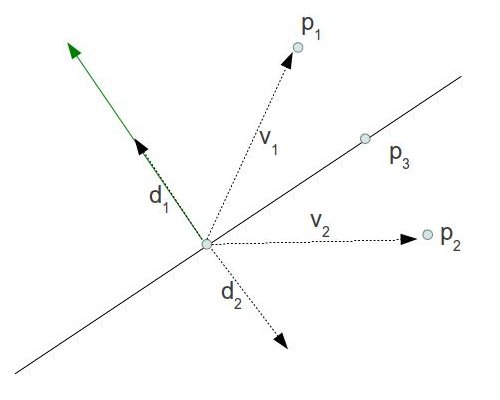
P₁ и P₂ расположены на различных половинах пространства, создаваемых плоскостью. Когда мы проецируем v₁ на зеленую нормаль, то мы получаем длину d₁. Умножаем эту длину на нормаль для получения самого d₁. Теперь вычитаем ее из P₁ для получения ее проекции на плоскости. Когда мы проецируем v₂ на зеленую нормаль, мы получаем длину d₂, но это отрицательное число. Умножаем ее на нормаль для получения самого d₂ (отрицательная длина означает обратный вектор). Теперь вычитаем ее из P₂ для получения ее проекции на плоскости. Вывод: этот способ всегда работает правильно, не зависимо от того, с какой стороны плоскости наша точка.

lighting_technique.cpp:142

#version 410 core

layout(triangles, equal_spacing, ccw) in;

uniform mat4 gVP;

struct OutputPatch
{
    vec3 WorldPos_B030;
    vec3 WorldPos_B021;
    vec3 WorldPos_B012;
    vec3 WorldPos_B003;
    vec3 WorldPos_B102;
    vec3 WorldPos_B201;
    vec3 WorldPos_B300;
    vec3 WorldPos_B210;
    vec3 WorldPos_B120;
    vec3 WorldPos_B111;
    vec3 Normal[3];
    vec2 TexCoord[3];
};

in patch OutputPatch oPatch;

out vec3 WorldPos_FS_in;
out vec2 TexCoord_FS_in;
out vec3 Normal_FS_in;

vec2 interpolate2D(vec2 v0, vec2 v1, vec2 v2)
{
    return vec2(gl_TessCoord.x) * v0 + vec2(gl_TessCoord.y) * v1 + vec2(gl_TessCoord.z) * v2;
}

vec3 interpolate3D(vec3 v0, vec3 v1, vec3 v2)
{
    return vec3(gl_TessCoord.x) * v0 + vec3(gl_TessCoord.y) * v1 + vec3(gl_TessCoord.z) * v2;
}

void main()
{
    // Интерполируем атрибуты выходящей вершины через барецентрические координаты
    TexCoord_FS_in = interpolate2D(oPatch.TexCoord[0], oPatch.TexCoord[1], oPatch.TexCoord[2]);
    Normal_FS_in = interpolate3D(oPatch.Normal[0], oPatch.Normal[1], oPatch.Normal[2]);

float u = gl_TessCoord.x;
    float v = gl_TessCoord.y;
    float w = gl_TessCoord.z;

    float uPow3 = pow(u, 3);
    float vPow3 = pow(v, 3);
    float wPow3 = pow(w, 3);
    float uPow2 = pow(u, 2);
    float vPow2 = pow(v, 2);
    float wPow2 = pow(w, 2);

    WorldPos_FS_in = oPatch.WorldPos_B300 * wPow3 +
        oPatch.WorldPos_B030 * uPow3 +
        oPatch.WorldPos_B003 * vPow3 +
        oPatch.WorldPos_B210 * 3.0 * wPow2 * u +
        oPatch.WorldPos_B120 * 3.0 * w * uPow2 +
        oPatch.WorldPos_B201 * 3.0 * wPow2 * v +
        oPatch.WorldPos_B021 * 3.0 * uPow2 * v +
        oPatch.WorldPos_B102 * 3.0 * w * vPow2 +
        oPatch.WorldPos_B012 * 3.0 * u * vPow2 +
        oPatch.WorldPos_B111 * 6.0 * w * u * v;

    gl_Position = gVP * vec4(WorldPos_FS_in, 1.0);
}

Это содержание TES с выделенными изменениями. Нормаль и координаты текстуры интерполируются так же, как и раньше. Для того, что бы вычислить позицию в мировом пространстве, мы включаем барецентрические координаты в выражения для треугольника Безье из раздела теории. Встроенная функция pow() используется для вычисления числа в заданной степени. Мы преобразовываем мировые координаты в пространство клипа, а дальше все как обычно.