Урок 30 - Основы Тесселяции
Внимание: текстуры цвета и смещения, используемые в демо, были созданы Ben Cloward.
Тесселяция - это новая захватывающая возможность OpenGL 4.x. Главная проблема, которую решает тесселяция, - это статическая природа 3D моделей, выражающаяся в их деталях и количестве полигонов. Идея в том, что когда мы близко смотрим на сложную модель, такую как человеческое лицо, мы предпочитаем использовать высоко-детализированную модель, которая будет учитывать мелкие детали (неровность кожи и прочее). Чем более подробно сделана модель, тем из большего числа треугольников она составлена, а значит потребуется больше компьютерных вычислений для обработки. Когда мы рендерем ту же модель с большого расстояния, то мы предпочтем низко-детализированную модель и не станем тратить лишние компьютерные силы на нее. В этом и заключается балансирование ресурсов GPU и переопределение большинства ресурсов на ближайшую к камере область, на которой мелкие детали лучше видны.
Идин из способов решить эту проблему - использовать существующую возможность OpenGL генерировать одну и туже модель в различных уровнях детализации (levels of detail (LOD)). Например, высоко, средне и низко детализированная. Затем мы сможем выбирать версию в зависимости от расстояния до камеры. Хотя это и потребует от моделера больше сил, все равно может не хватить гибкости. То, что мы хотим сделать - начать с низкополигонной модели и делить каждый треугольник на ходу на меньшие треугольники. Это, в двух словах, и есть тесселяция. Мы в состоянии сделать это динамически на GPU и затем выбрать уровень детализации на треугольник - вот для чего тесселяция участвует в конвейере OpenGL 4.x.
Тесселяция была определена и интегрирована в спецификацию OpenGL после нескольких лет исследований и в академиях и в индустрии. Ее дизайн вобрал геометрию поверхностей, кривую Безье и разделение. Мы покорим тесселяцию в 2 этапа. В этом уроке мы фокусируемся на новом устройстве конвейера для того, что бы настроить и запустить тесселяциб не сильно вдаваясь в математическую часть. Сам метод будет не трудным, но он раскроет все используемые компоненты. В следующем уроке мы изучим часть Безье и увидим, как применить ее в методе тесселяции.
Давайте рассмотрим как тесселяция была включена в графический конвейер. Центральные компоненты, ответственные за тесселяцию, - 2 новых этапа шейдеров, а между ними фиксированная функция, которая может быть только чуть-чуть изменена. Первый этап называется Tessellation Control Shader (управляющей тесселяцией шейдер) (TCS), фиксированная функция называется Primitive Generator (генератор примитивов) (PG) и последний шейдер - Tessellation Evaluation Shader (определяющий тесселяцию шейдер) (TES). На следующей диаграмме показано их расположение в конвейере:
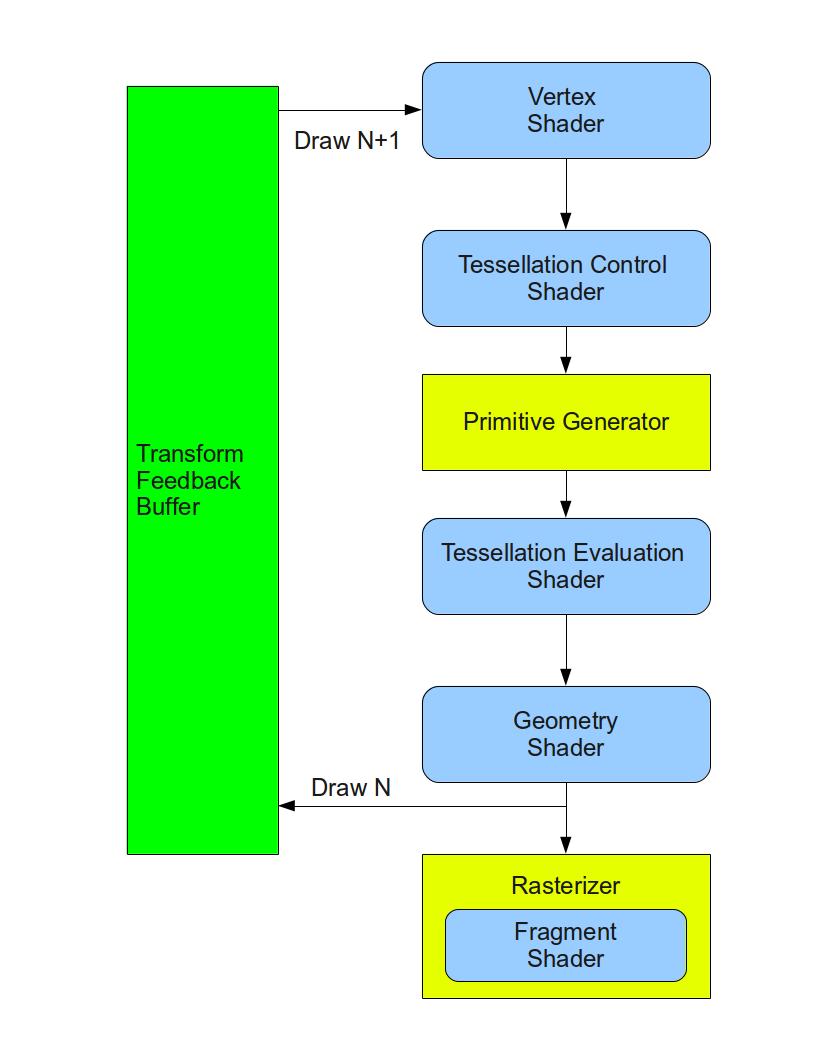
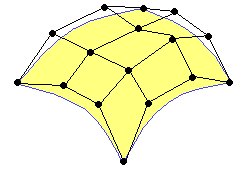
TCS работает с группой вершин, называемых Control Points (CP). CPs не составляют какого-то конкретного полигона типа треугольника, прямоугольника, пятиугольника или какого-то еще. Вместо этого они определяют поверхность. Она обычно определяется некоторой полиномной формуле, и идея в том, что перемещая CP, мы создаем эффект на главной поверхности. Вы, наверное, уже знакомы с графическим по, которое позволяет вам определять поверхности или кривые, используя набор CPs, и изменять их перемещая CPs. Группа CPs обычно называется Патчем (Patch). Желтая поверхность на следующем изображении определена патчем с 16 CPs:
TCS принимает на вход патч и выдает его же. Разработчик имеет возможность добавить в шейдер изменения CPs или даже добавить / удалять их. Кроме выходного патча управляющий шейдер вычисляет набор чисел, называемый Уровень тесселяции (Tessellation Levels) (TL). TL определяет уровень детализации - как много создать треугольников для патча. Так как все это происходит в шейдере, то у разработчика широкий выбор в алгоритмах для вычисления TLs. Например, мы можем решить, что TL будет равным 3, если растеризация треугольника будет покрывать менее 100 пикселей, 7 в случае от 101 до 500 пикселей и 12.5 для меньшего числа (мы еще увидим как значение TL приводит к более грубой или точной тесселяции). Другой алгоритм может быть основан на расстоянии до камеры. Прекрасный момент в этом то, что каждый патч может получить различный TLs в зависимости от своих характеристик.
После завершения TCS наступает время фиксированной функции PG, чья работа - это само разделение. Это обычно наиболее трудная часть для новичков. Идея в том, что PG на самом деле не разбивает выходящий из TCS патч. Фактически она даже не имеет к нему доступ. Вместо этого она принимает TLs разделяет, что называется областью Domain. Область может бить или нормированным (в отрезке от 0.0-1.0) прямоугольником с 2D координатами или равностороннем треугольником, определенным 3D барицентрическими координатами:
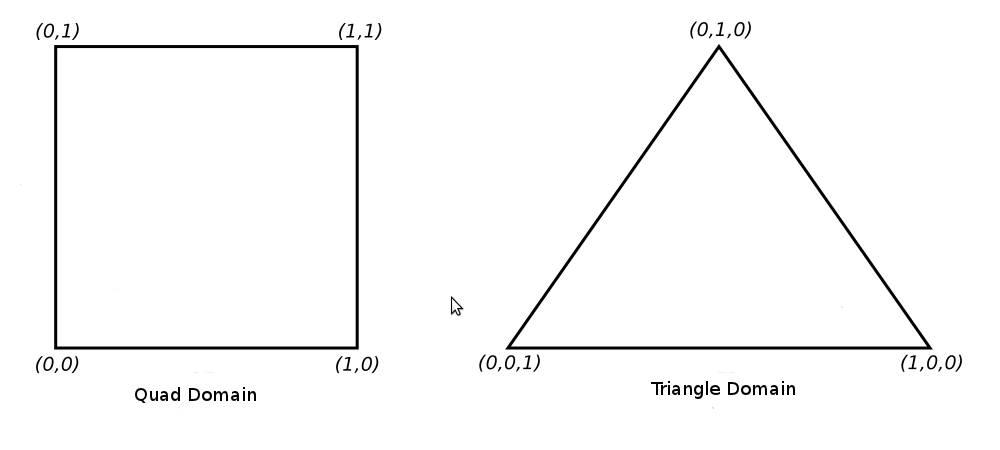
Барицентрические координаты (Barycentric coordinates) треугольника - это метод определения позиции внутри треугольника как комбинация веса трех вершин. Вершины треугольника задаются как U, V и W и при приближении позиции к одной из вершин ее вес увеличивается, а у других - уменьшается. Если позиция полностью совпадает с вершиной, то ее вес равен 1, а у остальных двух - 0. Например, барицентрические координаты U равны (1,0,0), для V (0,1,0) и у W (0,0,1). Центр треугольника по барицентрическим координатам в (1/3,1/3,1/3). Интересное свойство барицентрических координат в том, что если мы сложим все компоненты барицентрических координат, то получим 1 абсолютно для каждой точки. Для простоты фокусируемся на треугольной области.
PG принимает TLs и, основываясь на их значениях, генерирует набор точек внутри треугольника. Каждая точка определяется ее барицентрическими координатами. Разработчик может изменить выходящую топологию на точки или треугольники. Если выбраны точки, тогда PG просто отправит их дальше по конвейеру для растеризации их как точки. Если треугольники, тогда PG соединит все точки вместе так, что лицевая сторона треугольника тесселируется с меньшими треугольниками.:

В общем TLs сообщает PG количество сегментов на выходящей стороне треугольника и количество колец в сторону центра
Так как же маленькие треугольники на изображении выше относятся к патчу, который мы видели ранее? Что ж, это зависит от того, что вы собираетесь сделать с тесселяцией. Одна очень простая возможность (и еще одна представлены в этом уроке) - это пропускать все понятия изогнутых геометрических поверхностей и их полиномиальные представления и сказать, что треугольники из вашей модели будут просто отображены на патче. В этом случае 3 треугольные вершины станут нашими 3 CPs и оригинальный треугольник будет и входящим и выходящим патчем в TCS. Мы используем PG для тесселяции треугольной области и создания маленьких "общих" треугольников, представленных барицентрическими координатами и используя линейную комбинацию этих координат (т.е. умножая их на атрибуты оригинального треугольника) с целью тесселяции треугольников в оригинальной модели. В следующем уроке мы увидим настоящее использование патчей и представление геометрических поверхностей. В любом случае запомните, что PG игнорирует и входной и выходящий патчи TCS. Он только заботится о TLs для патча.
Итак, после того, как PG завершит разделение треугольной области, нам все еще требуется кто-то, кто принял бы результат разделения и что-нибудь сделал с ним. Кроме того, PG не имеет доступа к патчу. Он просто выдает барицентрические координаты и их связь. Войдем в TES. Этот шейдерный этап имеет доступ и к вышедшему из TCS патчу и к барецентрическим координатам, которые генерировал PG. PG запускает TES на каждую барецентрическую координату и работа TES состоит в генерации вершин для этих точек. Так как TES имеет доступ к патчу, он может брать из него данные, такие как позиция, нормаль и прочее, и использовать их для генерации вершин. После того, как PG запустит TES для каждых трех барецентрических координат "маленького" треугольника, он примет три вершины созданные TES и отправит их дальше на растеризацию.
TES похож на VS тем, что он тоже всегда принимает только единственный элемент на вход (барецентрические координаты) и единственный на выход (вершина). TES не может генерировать больше одной вершины за вызов, но может решить отбросить. Главная цель TES в тесселяции в OpenGL является предположительная оценка уравнения поверхности в данной области расположения. Простыми словами это означает размещение барецентрических координат в полиноме, который представляет поверхность и вычисляет результат. Результат - это позиция новой вершины, которая может быть преобразована и проецирована как обычно. Как вы видите, когда идет работа с геометрическими поверхностями, чем выше мы выбираем TL, тем больше положений в области мы получим, и оценивая их в TES, мы получим больше вершим при лучшем представлении настоящей математической поверхности. В этом уроке оценка уравнения поверхности будет простой линейной комбинацией.
После прохода TES по позиции области, PG принимает новые вершины и посылает их как треугольники в следующий этап конвейера. После TES наступает время для GS или растеризатора, а дальше как обычно.
Давайте подведем итоги:
- VS запускается для каждой вершины в патче. Патч получает несколько CPs из вершиного буфера (верхний предел определяется драйвером и GPU).
- TCS принимает вершины, которые были обработаны VS и генерирует выходной патч. Кроме того, он генерирует TLs.
- Основываясь на настроенной области, TLs получает из TCS заданную выходную топологию, и PG создает позиции области и их связи.
- TES вызывается для всех созданных позиций области.
- Примитивы, которые были созданы в шаге 3, идут по конвейеру дальше. На выход из TES идут их данные.
- Обработка продолжается или в GS или в растеризаторе.
Прямиком к коду!
tutorial30.cpp:80
GLint MaxPatchVertices = 0;
glGetIntegerv(GL_MAX_PATCH_VERTICES, &MaxPatchVertices);
printf("Max supported patch vertices %d\n", MaxPatchVertices);
glPatchParameteri(GL_PATCH_VERTICES, 3);
Когда включена тесселяция (т.е. когда мы имеем или TCS или TES) конвейеру требуется знать, как много вершин включает в себя патч. Вспомним, что патч не обязательно имеет определенную геометрическую форму. Это просто список контрольных точек. Вызов glPatchParameteri() в коде выше сообщает конвейеру, что размер входящего патча будет равен 3. Количество может быть увеличено до ограничения драйвера в GL_MAX_PATCH_VERTICES. Это значение может меняться в зависимости от GPU / драйвера, поэтому мы получаем его через glGetIntegerv() и выводим на экран.
lighting_technique.cpp:26
#version 410 core
layout (location = 0) in vec3 Position_VS_in;
layout (location = 1) in vec2 TexCoord_VS_in;
layout (location = 2) in vec3 Normal_VS_in;
uniform mat4 gWorld;
out vec3 WorldPos_CS_in;
out vec2 TexCoord_CS_in;
out vec3 Normal_CS_in;
void main()
{
WorldPos_CS_in = (gWorld * vec4(Position_VS_in, 1.0)).xyz;
TexCoord_CS_in = TexCoord_VS_in;
Normal_CS_in = (gWorld * vec4(Normal_VS_in, 0.0)).xyz;
}
Это наш VS, и вся разница между этим и предыдущем в том, что мы больше не преобразуем локальные координаты в пространство клипа (через умножение на матрицу мировой проекции (WVP)). Причина в том, что в этом больше нет смысла. Мы собираемся создать множество новых вершин, которые все равно потребуется преобразовывать. Поэтому это действие отложено до TES.
lighting_technique.cpp:47
#version 410 core
// задаем количество CP в выходном патче
layout (vertices = 3) out;
uniform vec3 gEyeWorldPos;
// атрибуты входящих CP
in vec3 WorldPos_CS_in[];
in vec2 TexCoord_CS_in[];
in vec3 Normal_CS_in[];
// атрибуты выходящих CP
out vec3 WorldPos_ES_in[];
out vec2 TexCoord_ES_in[];
out vec3 Normal_ES_in[];
Это начало TCS. Он вызывается для каждой вершины в output патче, и мы начинаем с определения количества CP в выходящем патче. Затем мы определяем uniform-переменную, которая нам потребуется для вычисления TLs. После этого мы получаем несколько атрибутов для входящих и выходящих CP. В этом уроке мы используем одинаковую структуру и для входящих и выходящих патчей, но это не всегда хорошее решение. Каждая входящая и выходящая CP имеет мировую позицию, координаты текстуры и нормаль. Так как мы можем иметь более одной CP в входящем и выходящем патче, то каждый атрибут определен как массив через модификатор []. Это позволит нам свободно нумеровать любую CP.
lighting_technique.cpp:79
void main()
{
// Устанавливаем контрольные точки выходящего патча
TexCoord_ES_in[gl_InvocationID] = TexCoord_CS_in[gl_InvocationID];
Normal_ES_in[gl_InvocationID] = Normal_CS_in[gl_InvocationID];
WorldPos_ES_in[gl_InvocationID] = WorldPos_CS_in[gl_InvocationID];
Мы начинаем главную функцию TCS с копирования входящих CP в выходящие CP. Эта функция вызывается один раз для выходящей CP, и встроенная переменная gl_InvocationID хранит индекс текущего вызова. Порядок вызовов не определен, поскольку GPU возможно распределяет CPs по своим ядрам и запускает процесс параллельно. Мы используем gl_InvocationID как индекс и в входящем и в выходящем патчах.
lighting_technique.cpp:86
// Вычисление расстояния от камеры до трех контрольных точек
float EyeToVertexDistance0 = distance(gEyeWorldPos, WorldPos_ES_in[0]);
float EyeToVertexDistance1 = distance(gEyeWorldPos, WorldPos_ES_in[1]);
float EyeToVertexDistance2 = distance(gEyeWorldPos, WorldPos_ES_in[2]);
// Вычисление уровня тесселяции
gl_TessLevelOuter[0] = GetTessLevel(EyeToVertexDistance1, EyeToVertexDistance2);
gl_TessLevelOuter[1] = GetTessLevel(EyeToVertexDistance2, EyeToVertexDistance0);
gl_TessLevelOuter[2] = GetTessLevel(EyeToVertexDistance0, EyeToVertexDistance1);
gl_TessLevelInner[0] = gl_TessLevelOuter[2];
}
После создания выходящего патча мы вычисляем TL. TL может быть установлен различным для каждого выходящего патча. OpenGL предоставляет 2 строенных массива вещественного типа для TL: gl_TessLevelOuter (размер 4) и gl_TessLevelInner (размер 2). В случае треугольной области мы можем использовать только первых 3 члена gl_TessLevelOuter и первый член из gl_TessLevelInner (помимо треугольной области существуют прямоугольная и изолиния, которые дают различный доступ к массиву). gl_TessLevelOuter[] приблизительно определяет количество сегментов на каждой стороне, а gl_TessLevelInner[0] грубо определяет, как много колец будет содержать треугольник. Если мы определим вершины треугольника как U, V и W, то соответствующая сторона для каждой вершины будет той, которая ее противоположна:
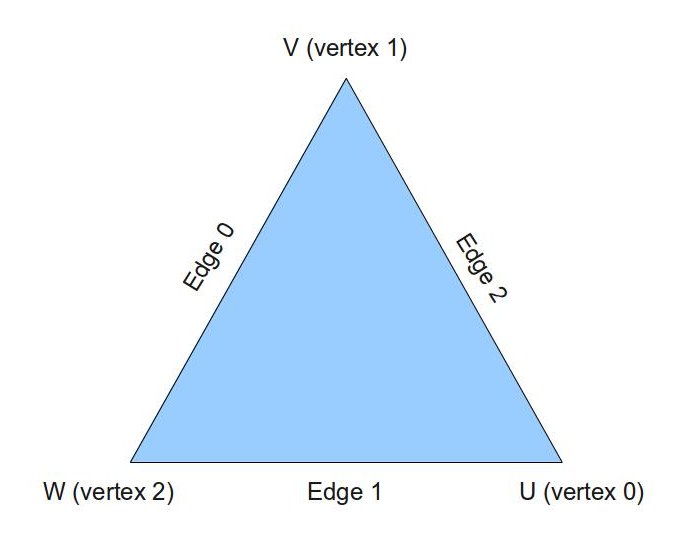
Алгоритм, который мы использовали для вычисления TLs очень прост и основывается на расстоянии от вершины до камеры в мировом пространстве. Он реализован в функции GetTessLevel (смотри ниже). Мы вычисляем расстояние между камерой и всеми вершинами и вызываем GetTessLevel() 3 раза для обновления каждого члена gl_TessLevelOuter[]. Каждый вход отображается на сторону согласно изображению выше (TL стороны 0 идет в gl_TessLevelOuter[0] и т.д.) и TL для этой стороны вычисляется основываясь на расстоянии от камеры до двух вершин, которые ее создают. Внутренний TL выбирается таким же, как и TL стороны W.
Вы можете использовать любой алгоритм какой захотите для вычисления TLs. Например, один алгоритм предполагает размер итогового треугольника на экране в пикселях и устанавливает TLs так, что не один тесселируемый треугольник не станет меньше, чем данное число пикселей.
lighting_technique.cpp:60
float GetTessLevel(float Distance0, float Distance1)
{
float AvgDistance = (Distance0 + Distance1) / 2.0;
if (AvgDistance <= 2.0) {
return 10.0;
}
else if (AvgDistance <= 5.0) {
return 7.0;
}
else {
return 3.0;
}
}
Эта функция вычисляет TL для стороны, основываясь на расстоянии от камеры до 2-х вершин на этой стороне. Мы берем среднее значение и устанавливаем TL в 10 или 7 или 3. При увеличении расстояния мы предпочитаем уменьшать TL, что бы не тратить силы GPU впустую.
lighting_technique.cpp:101
#version 410 core
layout(triangles, equal_spacing, ccw) in;
Это начало TES. Ключевое слово 'layout' определяет 3 элемента конфигурации:
- triangles - область, над которой работает PG. 2 другие опции - это квадраты quads и изолиния isolines.
- equal_spacing означает, что стороны треугольника будут разделены на сегменты с одинаковой длиной (согласно TLs). Вы так же можете использовать fractional_even_spacing (четные) или fractional_odd_spacing (нечетные), которые предоставляют смягченный перенос длины, когда TL дает четное или нечетное целочисленное значение. Например, если вы используете fractional_odd_spacing и TL равен 5.1, то это значит, что будет 2 очень коротких сегмента и 5 больших. При росте TL вверх все 7 сегментов станут приблизительно одной длины. Когда TL достигнет 7, то 2 новых очень коротких сегмента будут созданы. fractional_even_spacing действует аналогично с четными значениями TLs.
- ccw означает, что PG будет проходить по треугольнику против часовой стрелки (так же можно использовать cw для часового порядка). Возможно вы спросите: почему мы идет в это направлении, когда наша лицевая сторона треугольника в часовом порядке? Причина в том, что модель для данного урока (quad2.obj) была создана в Blender в против часовом порядке. Я могу указать Assimp флаг 'aiProcess_FlipWindingOrder' во время загрузки модели и использовать 'cw' здесь. Я просто не хочу пока что изменять 'mesh.cpp'. Суть в том, что прежде чем что-то делать, задумайтесь, что же вы делаете.
Заметим, что вы можете так же указать каждый конфигурационный элемент с его собственным словом layout. В примере выше мы просто уменьшаем требуемое пространство.
lighting_technique.cpp:105
uniform mat4 gVP;
uniform sampler2D gDisplacementMap;
uniform float gDispFactor;
in vec3 WorldPos_ES_in[];
in vec2 TexCoord_ES_in[];
in vec3 Normal_ES_in[];
out vec3 WorldPos_FS_in;
out vec2 TexCoord_FS_in;
out vec3 Normal_FS_in;
TES может иметь uniform-переменные так же, как и другие типы шейдеров. Карта смещения - обычная карта высот, что означает, что каждый тексель представляет высоту этой позиции. Мы будем использовать ее для генерации неровностей на поверхности нашего меша. Кроме того, TES так же имеет доступ к содержимому выходящего из TCS патчу. Наконец, мы объявляем атрибуты наших выходящих вершин. Заметим, что модификатор массива не требуется здесь, поскольку TES всегда выдает только одну вершину.
lighting_technique.cpp:127
void main()
{
// Интерполирование атрибутов выходящих вершин, используя барецентрические координаты
TexCoord_FS_in = interpolate2D(TexCoord_ES_in[0], TexCoord_ES_in[1], TexCoord_ES_in[2]);
Normal_FS_in = interpolate3D(Normal_ES_in[0], Normal_ES_in[1], Normal_ES_in[2]);
Normal_FS_in = normalize(Normal_FS_in);
WorldPos_FS_in = interpolate3D(WorldPos_ES_in[0], WorldPos_ES_in[1], WorldPos_ES_in[2]);
Это главная функция TES. Давайте повторим все, что мы сделали, что бы дойти до сюда. Вершины меша были обработаны VS, а позиция и нормаль были найдены в мировом пространстве. TCS получил каждый треугольник как патч с тремя CP и просто передал их в TES. PG разделил равносторонние треугольники на маленькие треугольники и запустил TES для каждой созданной вершины. В каждом вызове TES мы можем получить доступ к барецентрическим координатам (или координатам тесселяции) вершины в 3D-векторе gl_TessCoord. Так как барецентрические координаты в треугольнике представляют комбинацию веса 3 вершин, мы можем использовать их для интерполяции всех атрибутов новой вершины. Функции interpolate2D() и interpolate3D() (ниже) делают следующее: они принимают атрибуты из CPs из патча и интерполируют их, используя gl_TessCoord.
lighting_technique.cpp:135
// Перемещаем вершину вдоль нормали
float Displacement = texture(gDisplacementMap, TexCoord_FS_in.xy).x;
WorldPos_FS_in += Normal_FS_in * Displacement * gDispFactor;
gl_Position = gVP * vec4(WorldPos_FS_in, 1.0);
}
Имея разделенный на маленькие треугольник оригинального меша, мы не сильно изменили внешний вид меша, поскольку маленькие треугольники в той же плоскости, что и большой треугольник. Мы хотим сместить (или переместить) каждую вершину в сторону, которая будет соответствовать содержанию нашей текстуре цвета. Например, если текстура хранит изображение кирпича или камня, мы хотели бы, что бы наши вершины двигались влодь стороны кирпича или камня. Что бы сделать это, нам потребуется дополнить нашу текстуру цвета картой смещения (displacement map). Существует множество инструментов и редакторов, которые создают карту смещения, и мы не собираемся вдаваться в подробности. Больше информации о ней в сети. Для использования карты мы просто берем сэмпл из нее используя текущие координаты текстуры, и это даст нам высоту текущей вершины. Затем мы смести вершину в мировом пространстве через умножение нормали вершины на ее высоту и через коэффициент смещения в виде uniform-переменной, которая может быть настроена через приложение. Поэтому каждая вершина перемещается вдоль своей нормали согласно ее весу. Наконец, мы умножаем новые координаты в мировом пространстве на матрицу проекции и устанавливаем значение в 'gl_Position'.
lighting_technique.cpp:117
vec2 interpolate2D(vec2 v0, vec2 v1, vec2 v2)
{
return vec2(gl_TessCoord.x) * v0 + vec2(gl_TessCoord.y) * v1 + vec2(gl_TessCoord.z) * v2;
}
vec3 interpolate3D(vec3 v0, vec3 v1, vec3 v2)
{
return vec3(gl_TessCoord.x) * v0 + vec3(gl_TessCoord.y) * v1 + vec3(gl_TessCoord.z) * v2;
}
Эти 2 функции интерполируют между тройкой 2D-векторов и 3D-векторов используя 'gl_TessCoord' как вес.
lighting_technique.cpp:277
bool LightingTechnique::Init()
{
...
if (!AddShader(GL_TESS_CONTROL_SHADER, pTessCS)) {
return false;
}
if (!AddShader(GL_TESS_EVALUATION_SHADER, pTessES)) {
return false;
}
...
Не забудьте компилировать 2 новых шейдера!
Демо
Демо в этом уроке показывает как тесселировать прямоугольную поверхность и смещать вершины вдоль камней на текстуре цвета. Вы можете использовать '+' и '-' на клавиатуре для обновления коэффициента смещения и через него управлять уровнем перемещения. Вы так же можете переключиться в режим каркаса (wireframe) через 'z' и увидеть, как текущие треугольники создаются процессом Тесселяции. Интересно так же наблюдать с различных дистанций в режиме каркаса и видеть, как уровень Тесселяции изменяется в зависимости от расстояния. Вот почему нам требуется TCS.