Урок 47 - Карты теней с направленным источником света
Авторские права: некоторые изображения взяты с Clipart Panda и ClipArtHut.
Алгоритм карты теней, который был рассмотрен в уроке 23 и уроке 24, использовал прожектор в качестве источника света. Сам алгоритм основан на идее рендера на карту теней из позиции источника света. Прожектор используется потому, что его поведение очень схоже со стандартной камерой - тоже имеет направление и позицию, а освещаемая область увеличивается при удалении от источника:
Тот факт, что прожектор имеет форму усеченного конуса упрощает нам жизнь - мы можем использовать ту же самую матрицу проецирования перспективы, что и для камеры. Довольно сложно было реализовать Карты теней с точечным источником света, но там мы справились с помощью рендера в кубическую текстуру. Хотя проекцию всё ещё требовалось проецировать.
Теперь давайте подумаем о направленном свете. Отличается он тем, что у него нет позиции, но есть направление. Обычно он используется для имитации солнца, которое благодаря своим размерам, испускает почти параллельные лучи:
В этом случае проекция перспективы не применима. Приветствуем ортогональную проекцию. Идея в том, что лучи не исходят из одной точки (камеры), а остаются параллельными. При этом теряется 3D эффект.
На следующем изображении слева мы видим куб с использованием проекции перспективы, а справа куб с ортогональной проекцией:
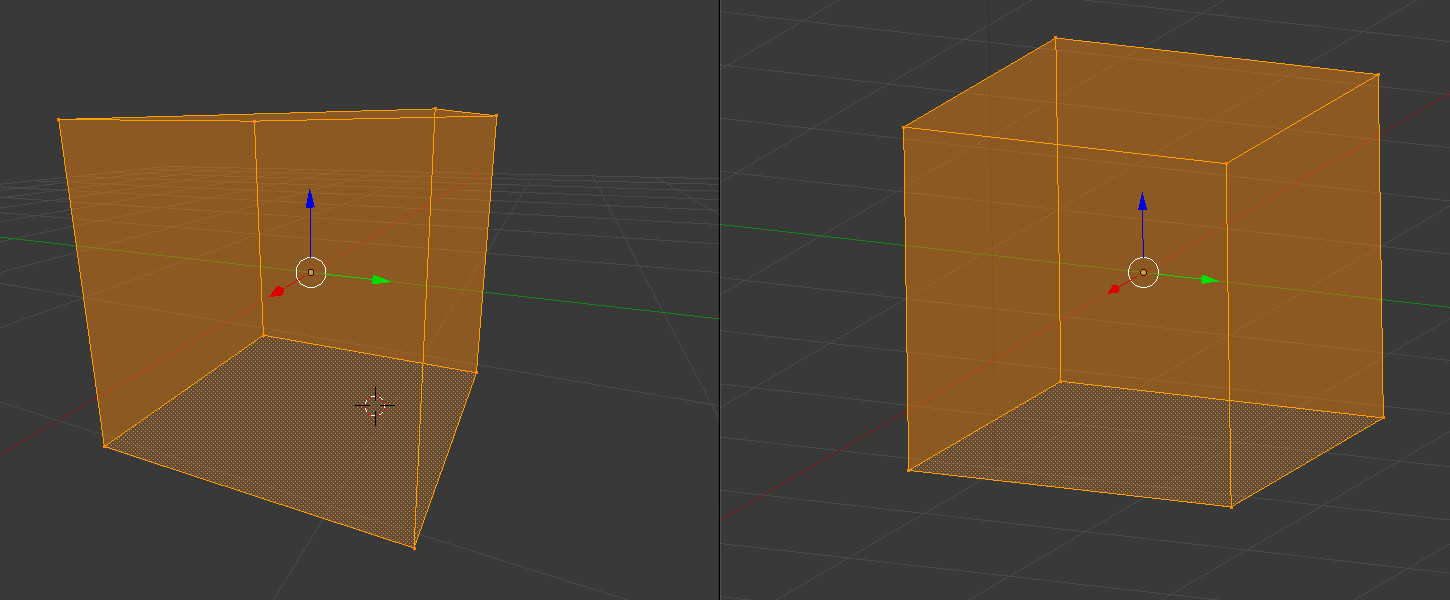
Куб слева похож на настоящий, выглядит как и дожен и создает ощущение глубины. В тоже время, куб справа не похож на настоящий, поскольку передняя и задняя грани одинаковы. Да, мы знаем, что из размеры одинаковы, но когда мы смотрим на них, то ожидаем, что передняя грань будет немного больше. Итак, как же ортогональная проекция может нам помочь? Что ж, вспомним, что проекция перспективы берет нечто похожее на усеченный конус и отображает его на нормированный куб (вершины которого имеют координаты от [-1,-1,-1] до [1,1,1]). После отображения координаты XY используются для нахождения координат текстуры (в нашем случае карты теней) и Z значения. Ортогональная проекция принимает обычный параллелепипед и отображает его на нормированный куб:
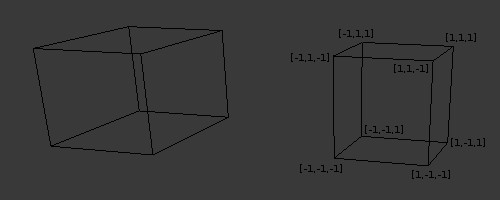
Теперь представьте лучи направленного света выходящими из передней грани куба и идущими параллельно до задней стенки. Если мы произведем отображение между параллелепипедом и нормированным кубом (вспомним, что мы называем это NDC пространством), то остальная часть построения карты теней не изменится.
Теперь давайте разберемся, как происходит отображение. У нас есть три отрезка вдоль осей XYZ, которые нужно отобразить в (-1,1). Упростим себе жизнь и разместим параллелепипед симметрично осям. Мы можем так сделать потому, что проецирование происходит после мировых преобразований, где мы вращаем и смещаем мир таким образом, что бы свет находился в начале координат и был направлен вдоль оси Z. Общий вид уравнения для отображения отрезка (a,b) в (c,d):
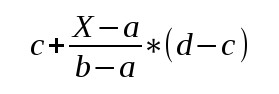
Где a<=X<=b. Произведем отображение на оси X. Произведем отображение по оси X. Подставим отрезки (-r,r) и (-1,1) в уравнении выше и получим (r означает "right" на оси X):
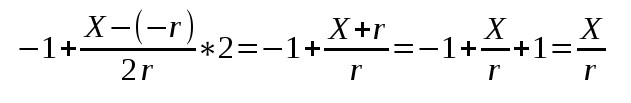
Аналогично для отображения по оси Y из (-t,t) в (-1,1):
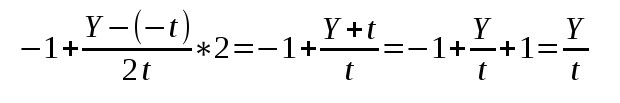
В случае оси Z нам нужно отобразить (n,f) (где n это ближняя плоскость, а f дальняя) на (-1,1):
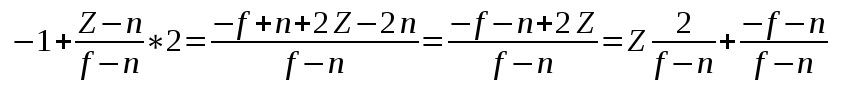
Теперь используя три уравнения отображения составим матрицу, для того что бы красиво их обернуть:
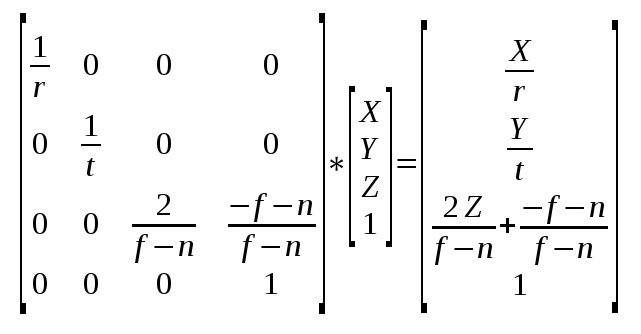
Сравните эту матрицу с той, которую мы создали для проецирования перспективы в уроке 12. Важное отличие в том, что элемент [3,2] (отсчет с нуля) равен 0, а не 1. Для деления перспективы было необходимо скопировать Z в позицию W. Это позволяло GPU выполнять разделение перспективы автоматически, в момент, когда всё делится на W (и это невозможно отключить). В случае ортогональной проекции W будет равно 1, эффективно отменяя эту операцию.
Когда будите работать с картой теней и направленным источником света, нужно быть осторожным с заданием параметров ортогональной проекции. С проекцией перспективы жизнь немного проще. FOW задает насколько широкой будет камеры, и по природе конуса, мы видим всё больше и больше с удалением от камеры (аналогично тому, как работают наши глаза). Мы также задаём дальнюю и ближнюю плоскости для обрезания на расстоянии. В большинстве случаев одни и те же значения FOW дают одинаково хороший результат. Но в случае ортогональной проекции у нас скорее параллелепипед, чем конус, и если не быть аккуратными, то мы можем "упустить" объект и ничего не отрендерить. Рассмотрим пример. На сцене ниже я задал ширину и высоту 20, а ближнюю и дальнюю -10 и 100 соответственно:
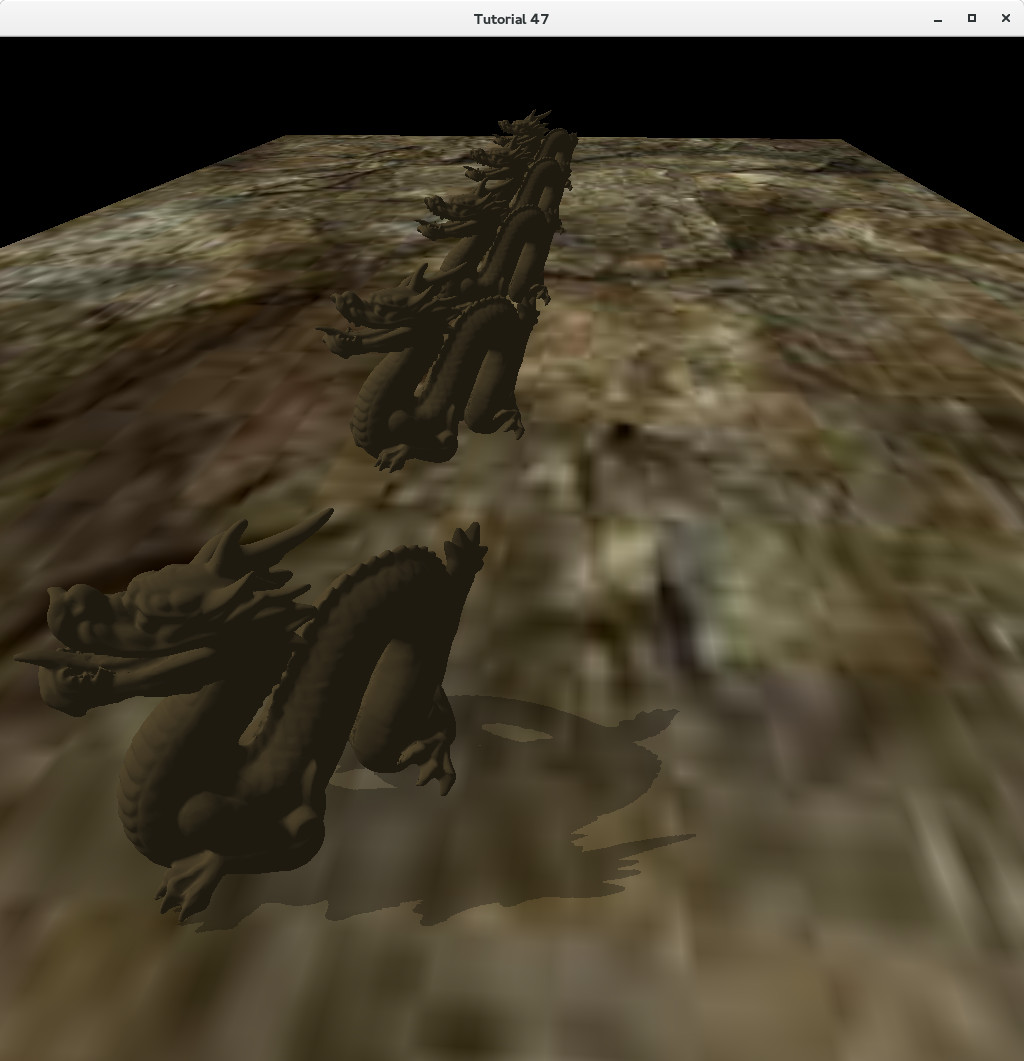
Проблема в том, что объекты находятся на расстоянии 30 друг от друга; проекция была не достаточно широкой для того, что бы захватить всю сцену (вспомним, что направление света ортогонально обзору, поэтому объекты разбросаны на широком поле относительно света). Теперь, давайте увеличим ширину и высоту до 200 (ближнюю и дальнюю оставим без изменений):
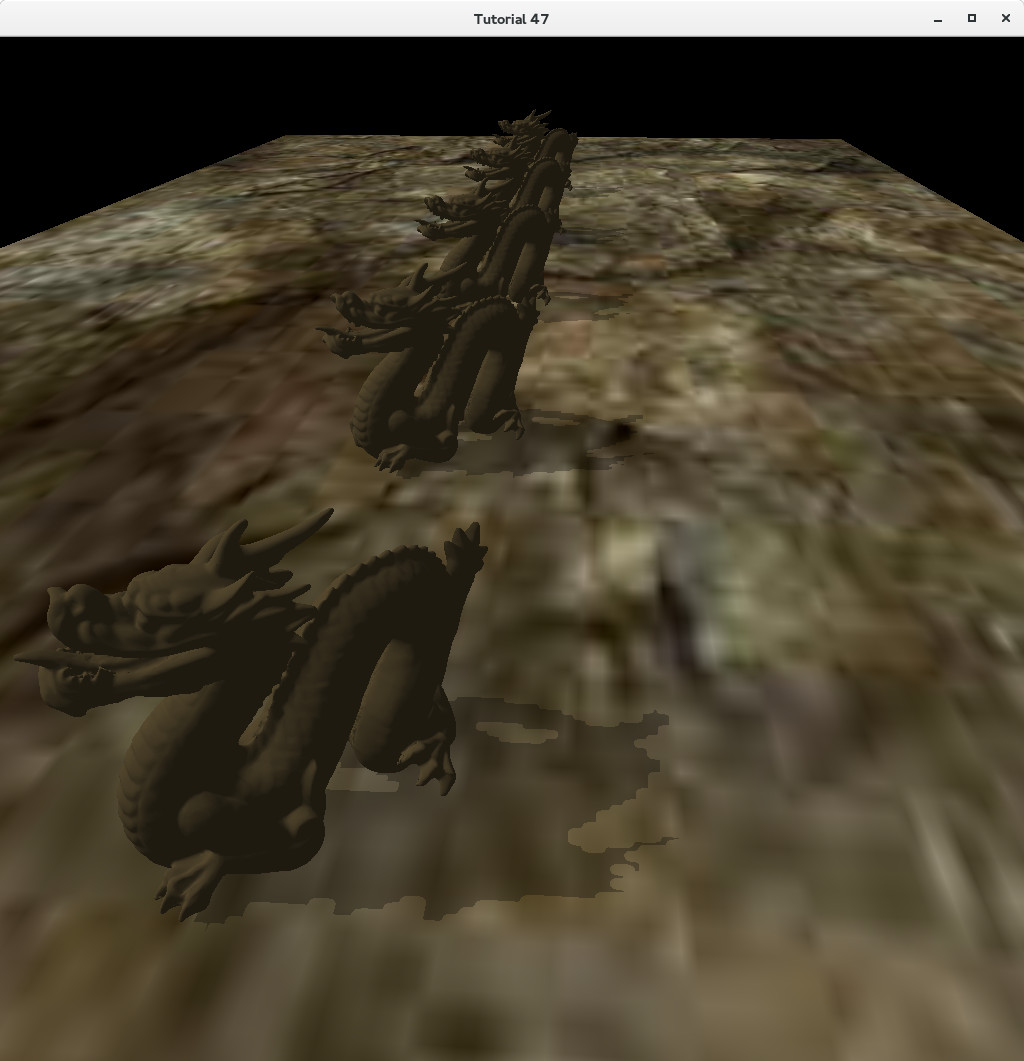
Теперь все объекты имеют тень. Хотя, у нас появилась новая проблема. Тени уже не выглядят так хорошо, как когда только один объект имел тень. Эта проблема называется Растеризация перспективы (Perspective Aliasing), и причина тому то, что многие пиксели в пространстве камеры (когда рендер идет из положения камеры) отображаются на один и тот же пиксель на карте теней. Из-за этого тени выглядят слегка блочными. Когда мы увеличили размеры ортогонального параллелепипеда, мы увеличили отношение сторон, потому что карта теней своих размеров не изменила. Растеризацию можно избежать увеличив размер карты теней, но не слишком сильно из-за больших затрат памяти. В будущих уроках мы рассмотрим более сложные методики решения этой проблемы.
Прямиком к коду!
Главное отличие между картой теней с направленным и точечным источником заключается в выборе проекции. Поэтому я пройдусь только по необходимым изменениям. Прежде чем продолжить, убедитесь, что хорошо знакомы с уроком 23 и уроком 24, так как большая часть кода остается без изменений. Если у вас есть рабочая версия теней для точечного света, то потребуется внести лишь немного изменений.
matrix_3d.cpp:137
void Matrix4f::InitOrthoProjTransform(const PersProjInfo& p)
{
const float zRange = p.zFar - p.zNear;
m[0][0] = 2.0f/p.Width; m[0][1] = 0.0f; m[0][2] = 0.0f; m[0][3] = 0.0;
m[1][0] = 0.0f; m[1][1] = 2.0f/p.Height; m[1][2] = 0.0f; m[1][3] = 0.0;
m[2][0] = 0.0f; m[2][1] = 0.0f; m[2][2] = 2.0f/zRange; m[2][3] = (-p.zFar - p.zNear)/zRange;
m[3][0] = 0.0f; m[3][1] = 0.0f; m[3][2] = 0.0f; m[3][3] = 1.0;
}
Я добавил функцию выше в класс Matrix4f для инициализации матрицы ортогональной проекции. Обратим внимание, что в позициях (0,0) и (1,1) делится 2, а не 1. Причина в том, что в теории мы отображаем отрезки (-l,l) и (-t,t), но на практике у нас только ширина и высота, поэтому мы делим их на 2.
tutorial47.cpp:163
void ShadowMapPass()
{
m_shadowMapFBO.BindForWriting();
glClear(GL_DEPTH_BUFFER_BIT);
m_ShadowMapEffect.Enable();
Pipeline p;
<b>p.SetCamera(Vector3f(0.0f, 0.0f, 0.0f), m_dirLight.Direction, Vector3f(0.0f, 1.0f, 0.0f));
p.SetPerspectiveProj(m_shadowOrthoProjInfo);</b>
for (int i = 0; i < NUM_MESHES ; i++) {
p.Orient(m_meshOrientation[i]);
m_ShadowMapEffect.SetWVP(p.GetWVOrthoPTrans());
m_mesh.Render();
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);
}
void RenderPass()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
m_LightingTech.Enable();
m_LightingTech.SetEyeWorldPos(m_pGameCamera->GetPos());
m_shadowMapFBO.BindForReading(SHADOW_TEXTURE_UNIT);
Pipeline p;
<b>p.SetPerspectiveProj(m_shadowOrthoProjInfo);
p.Orient(m_quad.GetOrientation());
p.SetCamera(Vector3f(0.0f, 0.0f, 0.0f), m_dirLight.Direction, Vector3f(0.0f, 1.0f, 0.0f));
m_LightingTech.SetLightWVP(p.GetWVOrthoPTrans());
p.SetPerspectiveProj(m_persProjInfo); </b>
p.SetCamera(m_pGameCamera->GetPos(), m_pGameCamera->GetTarget(), m_pGameCamera->GetUp());
m_LightingTech.SetWVP(p.GetWVPTrans());
m_LightingTech.SetWorldMatrix(p.GetWorldTrans());
m_pGroundTex->Bind(COLOR_TEXTURE_UNIT);
m_quad.Render();
for (int i = 0; i < NUM_MESHES ; i++) {
p.Orient(m_meshOrientation[i]);
m_LightingTech.SetWVP(p.GetWVPTrans());
m_LightingTech.SetWorldMatrix(p.GetWorldTrans());
m_mesh.Render();
}
}
Выше полностью приведены проходы теней и рендера; они почти полностью такие же, как и для точечного света, поэтому мы не будем рассматривать их целиком. Всего пара отличий, который я должен упомянуть. Во-первых, я добавил свойство m_shadowOrthoProjInfo для того, что бы хранить данные для ортогональной проекции отдельно от переменных проекции перспективы. m_shadowOrthoProjInfo используется для настройки WVP точки обзора света.
Второе отличие в том, что мы помещаем камеру в начало координат для вычисления матрицы WVP. Поскольку направленный свет имеет только направление но не позицию, то нам не нужна эта переменная в мировой матрице. Нам нужно только повернуть мир таким образом, что бы свет был направлен вдоль оси Z.
lighting.fs:96
vec4 CalcDirectionalLight(vec3 Normal, <b>vec4 LightSpacePos</b>)
{
float ShadowFactor = CalcShadowFactor(LightSpacePos);
return CalcLightInternal(gDirectionalLight.Base, gDirectionalLight.Direction, Normal, <b>ShadowFactor</b>);
}
void main()
{
...
vec4 TotalLight = CalcDirectionalLight(Normal, <b>LightSpacePos</b>);
...
}
Шейдеры почти не изменились - нам нужно только вычислить коэффициент теней для направленного света.