Урок 46 - SSAO С Востановлением Глубины
В предыдущем уроке мы рассмотрели алгоритм Screen Space Ambient Occlusion. Мы использовали геометрический буфер, который содержал данные для первого этапа вычислений - координаты в пространстве экрана для каждого пикселя. В этом уроке мы собираемся попробовать вычислять позицию в пространстве экрана напрямую из буфера глубины. Преимущество этого подхода в том, что требуется значительно меньше памяти, потому что будет использоваться только одно число с плавающей точкой вместо трёх. Этот урок основывается на предыдущем, поэтому убедитесь, что вы полностью с ним разобрались. Приведенный код является только изменениями к предыдущему алгоритму.
В алгоритме SSAO мы сканируем окно пиксель за пикселем, создаём случайные точки вокруг каждого пикселя в пространстве экрана, проецируем их на ближнюю обрезающую плоскость и сравниваем их значение Z с самим пикселем в этой позиции. Позиция в пространстве экрана генерируется в геометрическом проходе в начале цикла рендера. Для того что бы правильно заполнить геометрический буфер позицией в пространстве экрана нам также нужен буфер глубины (иначе пиксели будут обновляться согласно порядку отрисовки вместо глубины). Мы может использовать только этот буфер для реконструкции всего вектора позиции, тем самым уменьшая требуемую для этого память (хотя нам и понадобится больше математики).
Давайте повторим этапы, требуемые для заполнения буфера глубины (а если вам нужно ещё больше деталей, посмотрите урок 12). Мы начинаем с позиции вершины в пространстве объекта, умножаем её на матрицу WVP, которая состоит из преобразований из локального-в-мировое, мирового-в-экранное пространство проецируя на ближнюю обрезающую плоскость. Результатом является 4D вектор с координатой Z в пространстве экрана в качестве четвёртого компонента. Мы считаем, что этот вектор на данный момент в пространстве клиппера. Этот вектор записывается в выходной вектор gl_Position из вершинного шейдера и GPU обрезает его первых три компоненты между -W и W (W это четвёртый компонент со значением Z из пространство экрана). Затем GPU выполняет деление перспективы, то есть вектор разделяется на W. Теперь первые три компоненты между -1 и 1, а последний компонент равен 1. Мы говорим, что вектор в пространстве нормированных координатах NDC (Normalized Device Coordinates).
Обычно вершина всего одна из трёх составляющих треугольник, поэтому GPU выполняет интерполяцию между тремя векторами NDC вдоль поверхности треугольника и вызывает фрагментный шейдер для каждого пикселя. На выходе из фрагментного шейдера GPU обновляет буфер глубины значением Z вектора NDC (согласно нескольким параметрам, таким как тест глубины, запись глубины и другие, которые должны быть правильно сконфигурированы). Важно вспомнить, что перед записью значения Z в буфер глубины, GPU переводит его из отрезка (-1,1) в (0,1). Мы должны правильно это обработать, иначе появятся графические аномалии.
В общем это вся математика касательно Z буфера. Теперь давайте предположим, что у нас есть значение Z, которое мы извлекли для пикселя и мы хотим воссоздать весь вектор из пространства экрана. Всё что нам необходимо для повтора этих шагов уже дано в описании выше, но прежде чем погружаться в детали убедимся, что математика в этот раз выражается числами и матрицами, а не словами. Поскольку нас интересует только позиция в пространстве экрана, мы можем рассмотреть только матрицу проецирования вместо полного набора WVP.
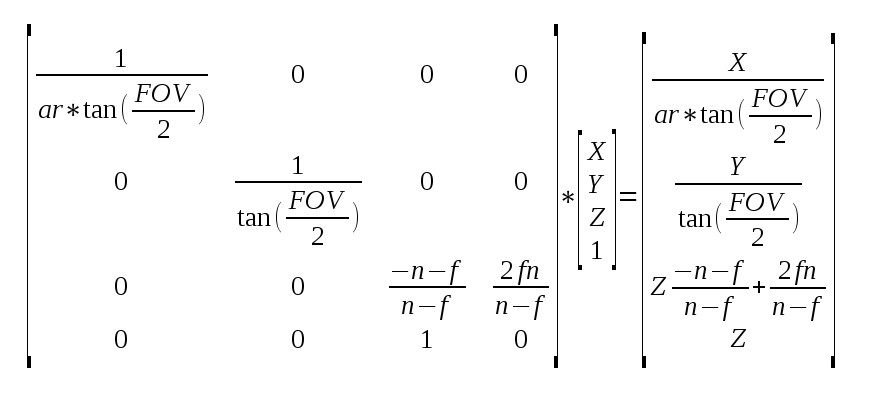
Выше мы видим проецирование вектора из пространства экрана в пространство клиппера (результат записан справа). Несколько замечаний:
- ar = Соотношение Сторон (ширина/высота)
- FOV = Угол обзора
- n = ближняя обрезающая плоскость
- f = дальняя обрезающая плоскость
Для упрощения записи дальнейших шагов обозначим значение в позиции (3,3) за S, а значение в позиции (3,4) за T. Это означает, что значение Z в NDC (вспомним про деление перспективы):
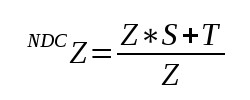
А поскольку мы переводим значение NDC из (-1,1) в (0,1), то в буфер глубины будет записано:
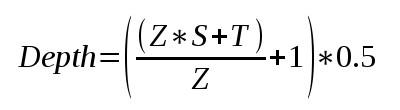
Теперь легко увидить, что мы можем извлечь значение Z из формулы выше. Я не стал описывать все промежуточные шаги, вы и сами можете их воспроизвести. Итоговый результат:
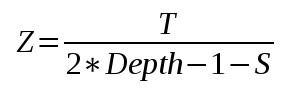
Теперь у нас есть позиция Z в пространстве экрана. Теперь разберёмся как мы можем получить X и Y. Вспомним, что после преобразования X и Y в пространство клиппера мы обрезаем до (-W,W) и делим на W (что есть Z в пространстве экрана). Теперь X и Y находятся в отрезке (-1,1); тоже самое касается значений всех интерполируемых пикселей треугольника. По факту, -1 и 1 отображаются в лево, право, верх и них экрана. Это означает, что для каждого пикселя на экране применяются следующие выражения (показано только для X, тоже самое для Y только без ar).
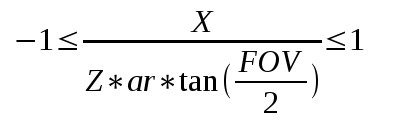
Это можно переписать следующим образом:
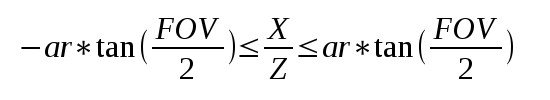
Обратим внимание, что левая и правая части неравенства - константы и могут быть вычислены приложением до вызова отрисовки. Это означает, что мы можем рисовать полноэкранный прямоугольник и подготовить 2D вектор с этими значениями для X и Y, и GPU будет интерполировать их по всему экрану. Когда мы доберёмся до пикселя, мы можем использовать интерполированные значения вместе с Z для вычисления как X, так и Y.
Прямиком к коду!
tutorial46.cpp:101
float AspectRatio = m_persProjInfo.Width / m_persProjInfo.Height;
m_SSAOTech.SetAspectRatio(AspectRatio);
float TanHalfFOV = tanf(ToRadian(m_persProjInfo.FOV / 2.0f));
m_SSAOTech.SetTanHalfFOV(TanHalfFOV);
Как я уже говорил, мы рассмотрим только отдельные изменения кода в сравнении с предыдущим уроков, связанные с востановлением глубины. Первое изменение - это то, что мы передаём соотношение сторон и тангенс половины угла обзора в технику SSAO. Выше уже показано как они вычисляются.
tutorial46.cpp:134
if (!m_depthBuffer.Init(WINDOW_WIDTH, WINDOW_HEIGHT, true, GL_NONE)) {
return false;
}
Затем мы инициализируем геометрический буфер (чей параметр m_gBuffer был переименован в m_depthBuffer с типом GL_NONE в качестве внутреннего формата. В этом случае будет создан только буфер глубины. Изучите файл io_buffer.cpp для больших подробностей внутренней работы класса IOBuffer.
tutorial46.cpp:181
void GeometryPass()
{
m_geomPassTech.Enable();
m_depthBuffer.BindForWriting();
glClear(GL_DEPTH_BUFFER_BIT);
m_pipeline.Orient(m_mesh.GetOrientation());
m_geomPassTech.SetWVP(m_pipeline.GetWVPTrans());
m_mesh.Render();
}
void SSAOPass()
{
m_SSAOTech.Enable();
m_SSAOTech.BindDepthBuffer(m_depthBuffer);
m_aoBuffer.BindForWriting();
glClear(GL_COLOR_BUFFER_BIT);
m_quad.Render();
}
Мы можем увидить переход от m_gBuffer к m_depthBuffer в проходах геометрии и SSAO. Также, нам больше не нужно вызывать glClear с битом буфера цвета, так как m_depthBuffer не хранит какой-либо информации и буфере цвета. На этом изменения в главном коде приложения закончены, и, как вы можете заметить, они минимальны. Самый сок всё-таки в шейдерах. Перейдём к ним.
geometry_pass.vs/fs
#version 330
layout (location = 0) in vec3 Position;
uniform mat4 gWVP;
// uniform mat4 gWV;
// out vec3 ViewPos;
void main()
{
gl_Position = gWVP * vec4(Position, 1.0);
// ViewPos = (gWV * vec4(Position, 1.0)).xyz;
}
#version 330
// in vec3 ViewPos;
// layout (location = 0) out vec3 PosOut;
void main()
{
// PosOut = ViewPos;
}
Выше мы видим измененный геометрический проход; всё что больше не требуется закоментированно. Поскольку мы пишем только в буфер глубины, всё что относится к позиции в пространстве экрана было выброшено. По факту, фрагментный шейдер теперь пуст.
ssao.vs
#version 330
layout (location = 0) in vec3 Position;
uniform float gAspectRatio;
uniform float gTanHalfFOV;
out vec2 TexCoord;
out vec2 ViewRay;
void main()
{
gl_Position = vec4(Position, 1.0);
TexCoord = (Position.xy + vec2(1.0)) / 2.0;
ViewRay.x = Position.x * gAspectRatio * gTanHalfFOV;
ViewRay.y = Position.y * gTanHalfFOV;
}
Согласно рассмотренной математике (в самом конце секции с теорией) нам необходимо создать что-то, что мы назовём лучом обзора в вершинном шейдере техники SSAO. Совместив с вычисленным значением Z в пространстве экрана в фрагментном шейдере мы сможем извлечь X и Y. Обратим внимание на то, как мы используем тот факт, что геометрией является полноэкранный прямоугольник, который идет от -1 до 1 по осям X и Y для создания точек -1/+1 * ar * tan(FOV/2) для X и -1/+1 * tan(FOV/2) и tan(FOV/2) для Y.
ssao.fs
#version 330
in vec2 TexCoord;
in vec2 ViewRay;
out vec4 FragColor;
uniform sampler2D gDepthMap;
uniform float gSampleRad;
uniform mat4 gProj;
const int MAX_KERNEL_SIZE = 64;
uniform vec3 gKernel[MAX_KERNEL_SIZE];
float CalcViewZ(vec2 Coords)
{
float Depth = texture(gDepthMap, Coords).x;
float ViewZ = gProj[3][2] / (2 * Depth -1 - gProj[2][2]);
return ViewZ;
}
void main()
{
float ViewZ = CalcViewZ(TexCoord);
float ViewX = ViewRay.x * ViewZ;
float ViewY = ViewRay.y * ViewZ;
vec3 Pos = vec3(ViewX, ViewY, ViewZ);
float AO = 0.0;
for (int i = 0 ; i < MAX_KERNEL_SIZE ; i++) {
vec3 samplePos = Pos + gKernel[i];
vec4 offset = vec4(samplePos, 1.0);
offset = gProj * offset;
offset.xy /= offset.w;
offset.xy = offset.xy * 0.5 + vec2(0.5);
float sampleDepth = CalcViewZ(offset.xy);
if (abs(Pos.z - sampleDepth) < gSampleRad) {
AO += step(sampleDepth,samplePos.z);
}
}
AO = 1.0 - AO/64.0;
FragColor = vec4(pow(AO, 2.0));
}
Первая вещь, которую мы делаем в фрагментном шейдере - это вычисление Z в пространстве экрана. Для этого используются те самые формулы, которые были изучены в секции с теорией. Матрица проекции уже использовалась с предыдущего урока и нам просто необходимо быть аккуратными при обращении к S и T в позициях (3,3) и (3,4). Вспомним, что индекс идет от 0 до 3 (а не от 1 до 4 согласно традиционной семантике матриц) и что матрица транспонированная, поэтому необходимо поменять местами номера строки и столбца для T.
Как только получен Z мы умножаем его на луч обзора для того, что бы получить X и Y. Дальше мы как и ранее создаём случайные точки и проецируем их на экран. Такой же трюк используется для вычисления глубины спроецированной точки.
Если вы всё сделали правильно, то вы должны получить точно такую же картинку, как и в предыдущем уроке… ;-)