Уроки по OpenGL с сайта OGLDev - Урок 27 - Billboarding и Геометрический шейдер

Урок 27 - Billboarding и Геометрический шейдер

Мы уже давно начали использовать вершинный и фрагментный шейдеры, но на самом деле мы пропустили один из типов, называемый Геометрический шейдер (Geometry Shader)(GS). Этот тип шейдеров был введен компанией Microsoft в DirectX10, а затем был добавлен в ядро OpenGL версии 3.2. В то время как VS запускается для вершин, а FS для пикселей, GS выполняется для примитива. Это означает, что если мы будем рисовать треугольники, то каждый вызов GS получит только один треугольник; если мы будем рисовать линии, то только 1 линию и т.д. Это дает GS уникальный взгляд на модель, в которой связи между вершинами доступны разработчику, позволяя строить новые методы, основываясь на этих знаниях.

Если вершинный шейдер в любой ситуации принимает только 1 вершину и выдает только 1 (т.е. он не может создавать или удалять вершины на ходу), то GS может изменять примитивы, проходящие через него. Изменения могут быть такими:

Изменять топологию входящих примитивов. GS может принимать примитивы любого типа, но выводить только списки точек, стрип линий и стрип треугольников (такая топология, как стрип, будет объяснена ниже).
GS принимает один примитив и может либо удалить его полностью, либо отправить на выход один или несколько примитивов (это значит, что он может выпускать и меньше и больше вершин, чем получает). Эта способность известна как growing geometry. Мы используем обе эти возможности в этом уроке.

Геометрический шейдер не обязателен. Если вы будете компилировать без GS, то примитивы будут просто переходить напрямую из вершинного шейдера в фрагментный шейдер. Вот почему мы смогли добраться до этой точки, не упоминая его.

Список треугольников строиться через тройку вершин. Вершины 0-2 становятся первым треугольников, вершины 3-5 -вторым и так далее. Для вычисления количества треугольников, генерируемых из любого количества вершин, просто делим количество вершин на 3 (опуская остальные). Стрипы треугольников более эффективны, поэтому что для получения нового треугольника, чаще мы хотим добавить только одну вершину, вместо 3. Когда вы добавляете 4-ю вершину, то второй треугольник будет строиться из вершин 1-3. Если вы добавите 5-ю вершину, то третий треугольник будет получен из вершин 2-4 и т.д. Поэтому начиная со 2 треугольника для каждой новой вершины будут браться еще и 2 предыдущие для нового треугольника. Вот пример:

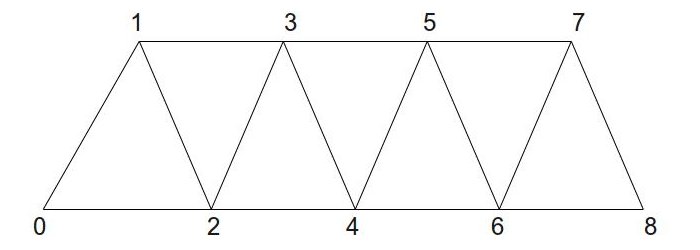
Как вы видите, 7 треугольников были созданы всего из 9 вершин. Если бы мы использовали список треугольников, то было бы только 3 треугольника.

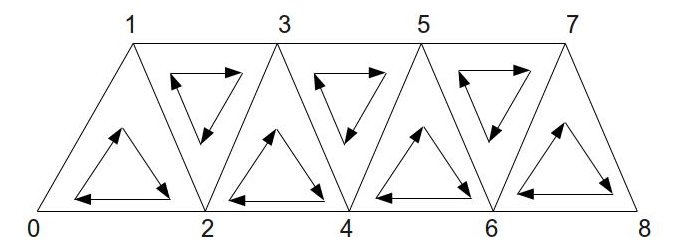
Стрип треугольников имеет важное свойство касательно порядка внутри треугольника - порядок обратен у нечетных треугольников. Это значит, что порядок таков: [0,1,2], [1,3,2], [2,3,4], [3,5,4] и т.д. Следующее изображение отражает порядок:

Теперь, когда вы познакомились с идеей геометрического шейдера, давайте рассмотрим, как он может помочь нам реализовать полезный и популярный метод, называемый billboarding. Billboarding - прямоугольник, который всегда направлен в камеру. При движении камеры по сцене billboard вращается за ней так, что вектор из billboard до камеры всегда перпендикулярен поверхности billboard. Аналог billboards в реальном мире могут служить рекламные щиты, которые расположены вдоль дорог так, что бы их видело как можно больше проезжающих мимо водителей. После получения прямоугольника на экране очень легко наложить на него текстуру с изображением монстра, дерева или чего-то еще и создать большое количество объектов на сцене, которые всегда повернуты в камеру. Billboards часто используют для создания леса, для создания которого требуется большое количество деревьев. Так как текстура billboard всегда направленна к камере, то зрителю будет казаться, что объект имеет настоящую глубину, хотя объект, на самом деле, абсолютно плоский. Каждый billboard требует всего 4 вершины, это гораздо дешевле полной модели.

В этом уроке мы создадим вершинный буфер и заполним его мировыми координатами billboards. Каждая позиция - просто точка (3D вектор). Мы передадим позиции в GS и соберем из каждой позиции прямоугольник. Это значит, что входящем типом GS будет точка, а выходящим - стрип треугольников. Воспользовавшись стрипом треугольников мы с легкостью соберем прямоугольник из 4 вершин:

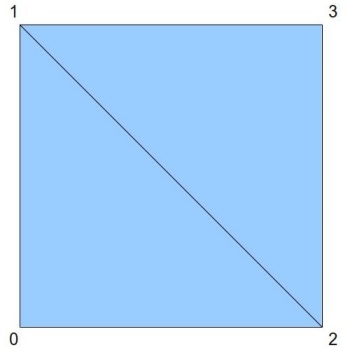
GS возьмет на себя заботу о том, что бы прямоугольник был повернут к камере, и подберет соответствующие координаты текстуры для каждой выходящей вершины. Фрагментный шейдер будет только брать сэмпл текстуры и выдавать итоговый цвет.

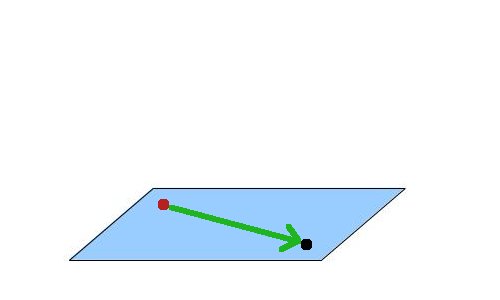
Давайте посмотрим, как направить billboard на камеру. На следующем изображении черная точка представляет камеру, а красная - позицию billboard. Обе точки в мировом пространстве, и хоть и кажется, что они обе расположены в плоскости параллельной XZ, это не обязательно так.

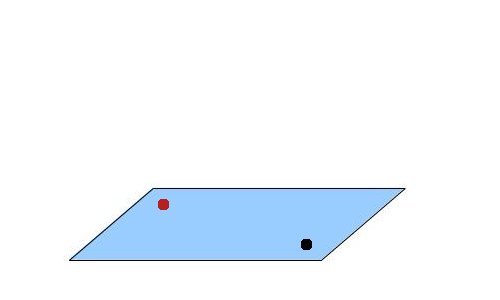
Сейчас мы проведем вектор из позиции billboard в камеру:

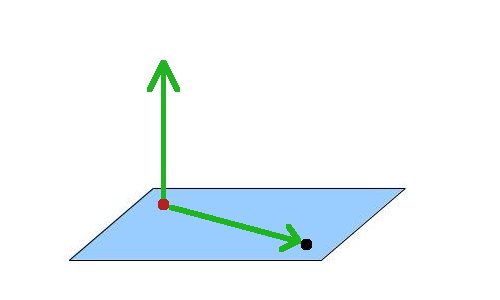
Далее мы добавим вектор (0,1,0):

Теперь произведем векторное произведение между 2 векторами. Результатом будет вектор, который перпендикулярен к поверхности созданной 2 векторами. Этот вектор имеет точно то направление, в котором мы хотим добавить точки и создать прямоугольник. Он будет перпендикулярен вектору из начальной позиции до камеры, то есть таким, каким мы и хотели. Посмотрим на эту же сцену с другой стороны и получим следующее: (желтый вектор - результат векторного произведения):

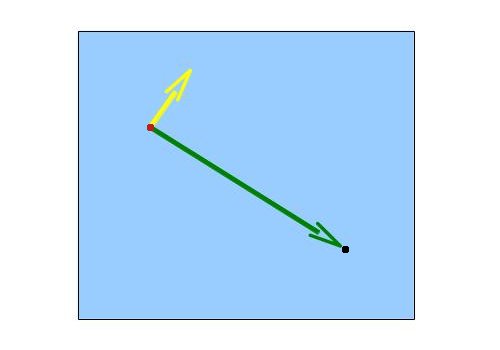
Одна из вещей, которая часто сбивает с толку программистов, - это в каком порядке находить векторное произведение (A умножить на B или B на A?). Эти 2 действия дают противоположный результат. Заранее знать получаемый результат предельно важно, поскольку нам требуется вывести вершины так, что бы 2 треугольника, которые образуют прямоугольник, были в часовом порядке, если смотреть на них из позиции камеры. Нам на помощь спешит правило левой руки. Это правило гласит, что если вы стоите в позиции billboard, и ваш указательный палец направлен в камеру, а ваш средний палец направлен вверх (прямо в небо), тогда ваш большой палец будет указывать на результат произведения указательного на средний пальцы (оставшиеся 2 пальца часто зажимают). В этом уроке мы будем называть результат векторного произведения "правым" вектором, потому, что он направлен направо, если смотреть на вашу руку из позиции камеры. Произведение среднего на указательный палец даст "левый" вектор.

(Мы используем правило левой руки из-за того, что мы работаем в левосторонней системе координат (Z растет при движении в сцену). В правосторонней системе координат наоборот).

Прямиком к коду!

billboard_list.h:27

class BillboardList
{
public:
    BillboardList();
    ~BillboardList();

    bool Init(const std::string& TexFilename);

    void Render(const Matrix4f& VP, const Vector3f& CameraPos);

private:
    void CreatePositionBuffer();

    GLuint m_VB;
    Texture* m_pTexture;
    BillboardTechnique m_technique;
};

Класс BillboardList инкапсулирует все, что вам потребуется для генерации billboards. Функция класса Init() принимает как параметр имя файла, который содержит изображение, которое будет отображаться на billboard. Функция Render() вызывается из главного цикла рендера и заботится от установлении всех значений и рендере billboard. Этой функции нужны 2 параметра: комбинация матрицы проекции и позиция камеры в мировом пространстве. Так как позиция billboard указана в мировом пространстве, то мы не нуждаемся в матрице преобразований. Класс имеет 3 private атрибута: вершинный буфер для хранения позиции billboards, указатель на текстуру для отображения на billboard и метод для billboard, который хранит соответствующие шейдеры.

billboard_list.cpp:80

void BillboardList::Render(const Matrix4f& VP, const Vector3f& CameraPos)
{
    m_technique.Enable();
    m_technique.SetVP(VP);
    m_technique.SetCameraPosition(CameraPos);

    m_pTexture->Bind(COLOR_TEXTURE_UNIT);

    glEnableVertexAttribArray(0);

    glBindBuffer(GL_ARRAY_BUFFER, m_VB);
    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(Vector3f), 0);   // position

    glDrawArrays(GL_POINTS, 0, NUM_ROWS * NUM_COLUMNS);

    glDisableVertexAttribArray(0);
}

Эта функция разрешает использование методов billboard, устанавливает требуемые переменные состояния OpenGL и рисует точки, которые будут переделаны в прямоугольник в GS. В демо к уроку billboards стоят ровными рядами и колонками, что и объясняет наличие здесь умножения для получения количества точек в буфере. Заметим, что мы используем список точек как входящая топология. GS перестроит из позже.

billboard_technique.h:24

class BillboardTechnique : public Technique
{
public:

    BillboardTechnique();

    virtual bool Init();

    void SetVP(const Matrix4f& VP);
    void SetCameraPosition(const Vector3f& Pos);
    void SetColorTextureUnit(unsigned int TextureUnit);

private:

    GLuint m_VPLocation;
    GLuint m_cameraPosLocation;
    GLuint m_colorMapLocation;
};

Это интерфейс для метода billboard. Он требует только 3 параметра для работы: комбинация матрицы проекции, позиция камеры в мировом пространстве и номер модуля текстуры, к которому будет привязана текстура billboard.

billboard_technique.cpp:21

#version 330

layout (location = 0) in vec3 Position;

void main()
{
    gl_Position = vec4(Position, 1.0);
}

Это вершинный шейдер метода billboard, и поскольку большая часть преобразований в GS, то вы не можете использовать стандартный VS. В вершинном буфере только вектор позиции, и так как он уже указан в мировом пространстве, мы просто передаем его в GS. Вот и все.

billboard_technique.cpp:33

#version 330

layout (points) in;
layout (triangle_strip) out;
layout (max_vertices = 4) out;

Ядро метода billboard располагается в GS. Давайте пройдемся по коду часть за частью. Мы начинаем с объявления глобальных вещей, с использованием ключевого слова 'layout'. Мы говорим конвейеру, что входящая топология - список точек, а выходящая - стрип треугольников. Мы так же сообщаем ему, что мы будем выпускать не более 4 вершин. Это выражение используется для того, что бы дать подсказку об максимальном количестве вершин, которые будут выходить из GS. Знание этого ограничения поможет драйверу оптимизировать поведение GS для некоторых ситуаций. Так как мы знаем, что мы собираемся выпускать прямоугольник для каждой вершины, то мы объявляем максимальное количество равным 4.

billboard_technique.cpp:39

uniform mat4 gVP;
uniform vec3 gCameraPos;

out vec2 TexCoord;

GS принимает позицию в мировом пространстве, поэтому ему требуется только матрица проекции. Он так же нуждается в позиции камеры для нахождения ориентации. GS генерирует координаты текстуры для FS, что мы и должны явно указать.

billboard_technique.cpp:44

void main()
{
    vec3 Pos = gl_in[0].gl_Position.xyz;

Строка выше уникальна для GS. Так как он вызывается для полного примитива, мы имеем доступ для каждой из вершины, которая составляет его. Это производится через встроенную переменную 'gl_in'. Эта переменная - массив структур, которые, между прочим, хранят позицию, которая была записана в gl_Position в VS. Для получения доступа к ней мы используем индекс интересующей вершины. В нашем случае топология - список точек, поэтому внутри только 1 вершина. Мы получаем доступ через 'gl_in[0]'. Если бы топологией был бы треугольник, то мы бы могли написать 'gl_in[1]' и 'gl_in[2]'. Нам нужны только первые 3 компонента вектора, и мы выделяем их в локальную переменную через '.xyz'.

    vec3 toCamera = normalize(gCameraPos - Pos);
    vec3 up = vec3(0.0, 1.0, 0.0);
    vec3 right = cross(toCamera, up);

Здесь мы поворачиваем поверхность billboard к камере согласно объяснениям в конце раздела теории. Мы находим векторное произведение между вектором из точки до камеры и вектором вверх. Это нам даст вектор, который направлен вправо, если смотреть на точку из позиции камеры. Теперь мы "вырастим" прямоугольник вокруг точки.

    Pos -= (right * 0.5);
    gl_Position = gVP * vec4(Pos, 1.0);
    TexCoord = vec2(0.0, 0.0);
    EmitVertex();

    Pos.y += 1.0;
    gl_Position = gVP * vec4(Pos, 1.0);
    TexCoord = vec2(0.0, 1.0);
    EmitVertex();

    Pos.y -= 1.0;
    Pos += right;
    gl_Position = gVP * vec4(Pos, 1.0);
    TexCoord = vec2(1.0, 0.0);
    EmitVertex();

    Pos.y += 1.0;
    gl_Position = gVP * vec4(Pos, 1.0);
    TexCoord = vec2(1.0, 1.0);
    EmitVertex();

    EndPrimitive();
}

Точка в вершинном буфере считается серединой нижней границы прямоугольника. Нам требуется генерировать 2 однонаправленных треугольника из нее. Мы начинаем с движения в нижний левый угол прямоугольника. Это делается через вычитание половины "правого" вектора из точки. Далее мы находим позицию в пространстве клипа через умножение точки на матрицу проекции. Мы так же устанавливаем координаты текстуры в (0,0), потому, что мы планируем целиком покрыть поверхность текстурой. Для отправки свежей вершины далее по конвейеру мы вызываем встроенную функцию EmitVertex(). После того, как эта функция вызвана, переменная, которую мы отправили, объявлена не определенной, и мы можем записывать в нее новые данные. Аналогичным способом мы строим верхний левый и нижний правый углы прямоугольника. Это будет первым треугольником. Так как выходная топология GS стрип треугольников, то нам нужно указать всего 1 вершину для второго треугольника. Он будет построен из новой вершины и 2 предыдущих (которые являются диагоналями). Четвертая, и последняя, вершина будет верхним правым углом прямоугольника. В конце стрипа мы вызываем встроенную функцию EndPrimitive().

billboard_technique.cpp:77

#version 330

uniform sampler2D gColorMap;

in vec2 TexCoord;
out vec4 FragColor;

void main()
{
    FragColor = texture2D(gColorMap, TexCoord);

    if (FragColor.r == 0 && FragColor.g == 0 && FragColor.b == 0) {
        discard;
    }
}

FS крайне прост - большая часть его работы - взять сэмпл из текстуры через координаты текстуры, генерированные GS. Добавилась новая часть - встроенная функция 'discard', используемая для того, что бы выбросить пиксель целиком в некоторых ситуациях. Изображение из Doom, которое включено в этот урок, показывает монстра на черном фоне. Используя эту текстуру как есть, сделает некоторые части billboard непрозрачными, что будет выглядеть нелепо. Для избежания этого мы отбрасываем черный цвет. Это позволит нам оставить только пиксели, которые составляют само изображение монстра. Попробуйте отключить 'discard' и посмотрите на разницу.