Урок 21 - Прожектор
Прожектор - это третий и последний тип освещения, который мы изучим (по крайней мере на ближайшее время…). Он немного сложнее чем и направленный и точечный свет и заимствует некоторые понятия из обоих. Прожектор имеет позицию и эффект затухания при удалении от объекта (как и точечный свет) и направление (как и направленный свет). Но у прожектора есть и свой уникальный атрибут - он светит только в пределах конуса, который становится шире по мере движения света. Хорошим примером будет фонарик. Прожектор очень полезен, когда персонаж в игре изучает подземные пещеры или бежит из тюрьмы.
Мы уже изучили все, что потребуется для разработки прожектора. Последний кусок - эффект конуса. Посмотрим на изображение:
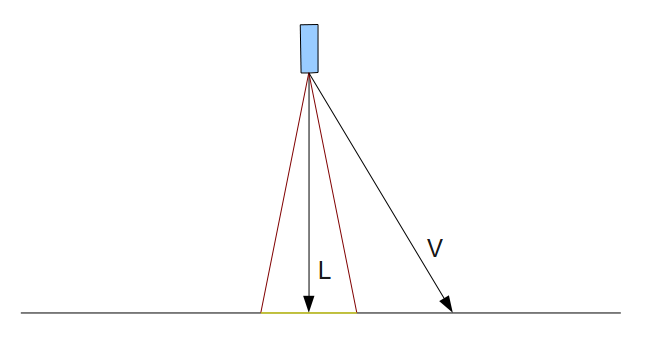
Направление прожектора задано черной стрелкой, идущей вниз. Мы хотим, что бы свет падал только в области, ограниченной 2 красными линиями. Скалярное произведение снова идет на помощь. Мы можем определить конус света как угол между любой из красных линий и направлением света (или как половина угла между красными линиями). Мы можем взять косинус 'C' этого угла и найти скалярное произведение между направлением света 'L' и вектором 'V'из источника света до пикселя. Если результат больше чем 'C' (вспомним, что косинус растет при уменьшении угла), то значит, что угол между 'L' и 'V' меньше, чем угол между 'L' и 2 красными линиями, который задает конус прожектора. В этом случае пиксель будет освещен, а если угол больше, пиксель не получит света от прожектора. В примере выше скалярное произведение между 'L' и 'V' позволит получить результат, который меньше чем скалярное произведение между 'L' и одной из красных линий (вполне очевидно что угол между 'L' и 'V' больше). Поэтому пиксель вне конуса не получит света от прожектора.
Если у нас будет такой подход в стиле "получит / не получит свет", то мы напишем дефектный прожектор, который имеет четкую границу между освещаемой и темной стороной. Это будет похоже на идеальный круг в полной темноте (не считая других источников света). Более реалистично когда свет постепенно затухает приближаясь к границе круга. Мы можем использовать скалярное произведение, которое мы нашли (что бы проверить будет ли пиксель освещен или нет), в качестве коэффициента. Мы уже знаем, что произведение будет равно 1 (т.е. максимум света), когда вектора 'L' и 'V' совпадают. Но теперь мы столкнемся с неприятной стороной функции косинуса. Угол прожектора не должен быть слишком большим, иначе свет будет слишком широким (и мы потеряем все преимущества прожектора. Например, давайте установим угол в 20 градусов. Косинус 20 - 0.939, но отрезок [0.939, 1.0] слишком мал для того, что бы быть коэффициентом. Не так много значений для интерполяции, которые глаз сможет заметить. Отрезок [0, 1] дал бы лучший результат.
Метод, который мы будем использовать для отображения маленького отрезка, полученного от прожектора, в большой [0, 1], описан ниже:
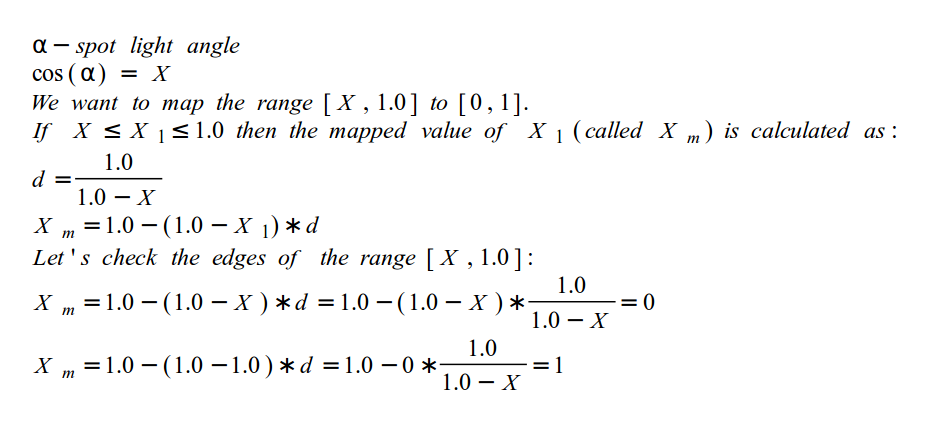
Принцип очень прост - вычисляем соотношение между меньшим и большим отрезками и умножаем указанный отрезок, который вы хотите отобразить, на этот коэффициент.
Прямиком к коду!
lighting_technique.cpp:68
struct SpotLight : public PointLight
{
Vector3f Direction;
float Cutoff;
SpotLight()
{
Direction = Vector3f(0.0f, 0.0f, 0.0f);
Cutoff = 0.0f;
}
};
Структура, которая определяет прожектор, наследуется от точечного света и добавляет 2 новых параметра: вектор направления и значение отсекания. Последнее означает максимальный угол между направлением света и вектором до пикселей, которые еще попадут под влияние света. Прожектор не затрагивает другие пиксели. Мы так же добавили в класс LightingTechnique массив адресов для шейдера (не показано здесь). Он позволит получить доступ к массиву прожекторов в шейдере.
lighting_technique.cpp:86
struct SpotLight
{
struct PointLight Base;
vec3 Direction;
float Cutoff;
};
...
uniform int gNumSpotLights;
...
uniform SpotLight gSpotLights[MAX_SPOT_LIGHTS];
Это аналогичная структура для прожектора в GLSL. Так как мы не можем здесь использовать наследование как в C++, мы используем структуру PointLight как член и добавлять атрибуты будем в него. Важное отличие здесь в том, что в C++ отсекание это значение угла, а в шейдере - его косинус, из-за того, что он одинаков для всех пикселей, и нет необходимости вычислять его вновь и вновь. Мы так же объявляем массив прожекторов и указываем их количество, названное 'gNumSpotLights', для того, что бы приложение могло сообщить сколько прожекторов мы используем.
lighting_technique.cpp:146
vec4 CalcPointLight(struct PointLight l, vec3 Normal)
{
vec3 LightDirection = WorldPos0 - l.Position;
float Distance = length(LightDirection);
LightDirection = normalize(LightDirection);
vec4 Color = CalcLightInternal(l.Base, LightDirection, Normal);
float Attenuation = l.Atten.Constant +
l.Atten.Linear * Distance +
l.Atten.Exp * Distance * Distance;
return Color / Attenuation;
}
Функция для точечного источника прошла через небольшое изменение - она теперь принимает экземпляр структуры PointLight в качестве параметра вместо обращения к глобальному массиву. Это упрощает взаимодействие с прожектором. Других изменений нет.
lighting_technique.cpp:146
vec4 CalcSpotLight(struct SpotLight l, vec3 Normal)
{
vec3 LightToPixel = normalize(WorldPos0 - l.Base.Position);
float SpotFactor = dot(LightToPixel, l.Direction);
if (SpotFactor > l.Cutoff) {
vec4 Color = CalcPointLight(l.Base, Normal);
return Color * (1.0 - (1.0 - SpotFactor) * 1.0/(1.0 - l.Cutoff));
}
else {
return vec4(0,0,0,0);
}
}
Здесь мы вычисляем эффект прожектора. Мы начинаем с взятия вектора из позиции источника света до пикселя. И как часто это бывает, мы нормируем его для того, что бы он был готов для предстоящего скалярного произведения между этим вектором и направлением света (которое уже нормировано в приложении), и получаем косинус угла между ними. Затем мы сравниваем полученное значение с коэффициентом отсекая света. Это косинус угла между направлением света и вектором, который определяет круг света. Если косинус меньше, это значит, что угол между направлением света и вектором к пикселю вне круга. В этом случае эффект от прожектора равен 0. Это ограничит прожектор малым или большим кругом, в зависимости от значения отсекания. В другом случае мы вычисляем основной цвет как если бы у нас был точечный источник. Затем мы берем результат скалярного произведения, который только что нашли ('SpotFactor'), и помещаем в формулу, описанную выше. Она даст коэффициент, который будет линейно интерполироваться от 0 до 1. Мы умножим его на цвет света и получим итоговый цвет прожектора.
lighting_technique.cpp:169
...
for (int i = 0 ; i < gNumSpotLights ; i++) {
TotalLight += CalcSpotLight(gSpotLights[i], Normal);
}
...
В той же манере, что и для точечного света, мы создаем цикл в главной функции, которая складывает влияние всех прожекторов в итоговый цвет пикселя.
lighting_technique.cpp:367
void LightingTechnique::SetSpotLights(unsigned int NumLights, const SpotLight* pLights)
{
glUniform1i(m_numSpotLightsLocation, NumLights);
for (unsigned int i = 0 ; i < NumLights ; i++) {
glUniform3f(m_spotLightsLocation[i].Color, pLights[i].Color.x, pLights[i].Color.y, pLights[i].Color.z);
glUniform1f(m_spotLightsLocation[i].AmbientIntensity, pLights[i].AmbientIntensity);
glUniform1f(m_spotLightsLocation[i].DiffuseIntensity, pLights[i].DiffuseIntensity);
glUniform3f(m_spotLightsLocation[i].Position, pLights[i].Position.x, pLights[i].Position.y, pLights[i].Position.z);
Vector3f Direction = pLights[i].Direction;
Direction.Normalize();
glUniform3f(m_spotLightsLocation[i].Direction, Direction.x, Direction.y, Direction.z);
glUniform1f(m_spotLightsLocation[i].Cutoff, cosf(ToRadian(pLights[i].Cutoff)));
glUniform1f(m_spotLightsLocation[i].Atten.Constant, pLights[i].Attenuation.Constant);
glUniform1f(m_spotLightsLocation[i].Atten.Linear, pLights[i].Attenuation.Linear);
glUniform1f(m_spotLightsLocation[i].Atten.Exp, pLights[i].Attenuation.Exp);
}
}
Эта функция обновляет программу шейдера массивом структур SpotLight. Это аналогично соответствующей функции для точечного света, с 2 новыми дополнениями. Вектор направления так же передается в шейдер, после нормирования. Кроме него значение отсекание поставляется как угол, но в шейдер идет его косинус (позволит сразу же сравнить результат скалярного произведения). Заметим, что функция cosf() принимает значение угла в радианах, поэтому мы используем макрос ToRadian для преобразования.