Урок 13 - Пространство камеры
В последней серии уроков мы видели 2 вида преобразований. Первый тип изменял позицию (движение), ориентацию (вращение) или размеры (масштабирование) объекта. Эти преобразования позволяли нам поместить объект в любую точку 3D пространства. Второй тип - эти проецирование перспективы, которое принимало позицию вершины в 3D пространстве и проецировало ее в 2D (т.е. на плоскость). Когда координаты переведены в 2D, то очень легко перевести координаты в пространство экрана. Эти координаты использовались для растеризации примитивов из которых и состоит объект (точки, линии или треугольники).
Последний элемент мозаики - это позиция камеры. Во всех предыдущих уроках мы считали, что камера расположена в начале координат. На самом же деле нам, конечно, хотелось бы свободы перемещения камеры в любую точку, и проекция вершин должна происходить на некую плоскость перед камерой. Это задаст правильную связь между камерой и объектами на экране.
На следующем изображении мы видим камеру, расположенную задом к нам. Перед ней есть виртуальная 2D плоскость, и шар проецируется на нее. Если камера наклоняется, то и плоскость наклоняется так же. Так как обзор камеры ограничен ее же углом обзора, то видимая часть (бесконечной) плоскости - это прямоугольник. Все что вне его, обрезается. Наша цель - перенести прямоугольник на экран.
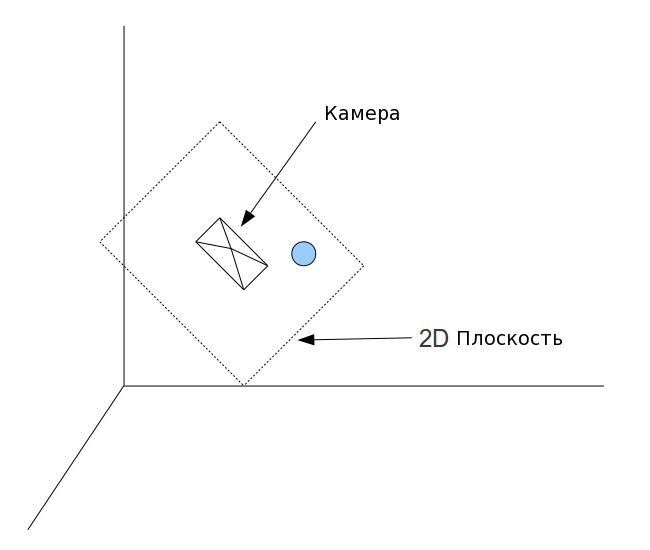
Теоретически, возможно генерировать преобразование, которое будет брать объект из 3D пространства и проецировать его на 2D плоскость, находящуюся прямо перед камерой, расположенной в произвольной позиции. Хотя такие математические вычисления гораздо сложнее всего, что мы видели ранее. Гораздо проще когда камера находится в начале координат и направленна в сторону уменьшения оси Z. Например, объект находится в (0,0,5), а камера в (0,0,1) и направленна противоположно оси Z (т.е. прямо на объект). Если мы подвинем и камеру и объект на одно расстояние, тогда относительное расстояние и ориентация (в значении направления камеры) останутся теми же самыми, как и в старом положении. Перемещение всех объектов на сцене в одном направлении позволит нам рендерить сцену правильно, при этом будут использоваться уже изученные методы.
Предыдущий пример слишком прост, поскольку камера уже направлена правильно. Но что произойдет, если камера направлена куда-то еще? Давайте посмотрим на следующее изображение. Для ясности здесь изображена 2D система координат, и мы смотрим на камеру сверху.
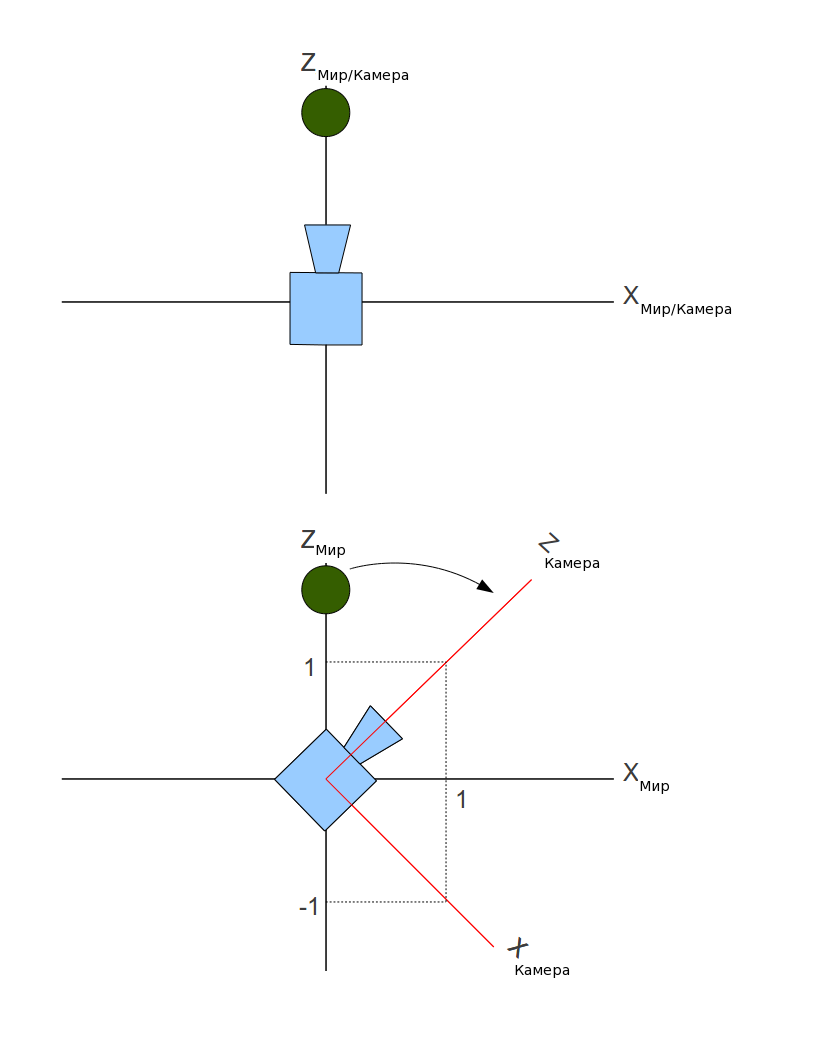
Камера была направлена в сторону убывания оси Z, а затем повернута на 45 градусов по часовой стрелке. Как вы видите, камера определяет свою собственную систему координат, которая может совпадать с мировой (верхнее изображение) или отличаться (нижнее). Поэтому у нас 2 системы координат одновременно. Первая 'мировая система координат', в которой располагаются объекты, и вторая это система координат камеры, со своими осями координат. Эти 2 системы называют 'мировое пространство' и 'пространство камеры'.
Зеленый шар расположен в (0,y,z) в мировых координатах. А относительно камеры он где-то в левой верхней четверти координатной системы (т.е. у него отрицательный X и положительный Z). Нам нужно вычислить его координаты относительно СК камеры. Тогда мы сможем позабыть об мировом пространстве и использовать только камерное. В пространстве камеры сама камера расположена в начале координат и направлена в сторону, обратную оси Z. Объекты соотносятся с камерой и могут рендерится используя уже изученные инструменты.
Поворот камеры на 45 градусов по часовой стрелке все равно, что и поворот объекта на 45 градусов против часовой. Движение объектов всегда противоположно движению камеры. Поэтому в целом нам нужно добавить 2 новых преобразования и включить их в конвейер, который у нас уже есть. Мы будем передвигать объекты так, что бы расстояние от них до камеры было бы таким же, как если бы камера располагалась в начале координат, и мы будем поворачивать объекты в направлении, противоположном вращению камеры.
Движение камеры устроено очень просто. Если координаты камеры (x,y,z), то преобразование позиции (-x, -y, -z). Причина тому проста - камера расположена в мировой СК с использованием перемещения, основанного на векторе (x,y,z) поэтому, что бы поместить ее обратно, необходимо преобразование, обратное данному. Вот как выглядит матрица преобразования:
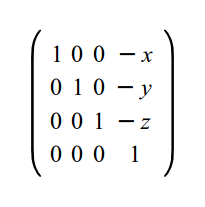
Следующий шаг - это поворот камеры на некоторые значения, указанные в мировых координатах. Нам требуется найти положение вершин в новой СК, устанавливаемой камерой. Поэтому логичен вопрос: как перейти из одной системы координат в другую?
Еще раз посмотрим на изображение выше. Мы можем сказать, что мировая система задана тремя линейно независимыми единичными векторами (1,0,0), (0,1,0) и (0,0,1). Линейная независимость означает, что мы не можем найти не равные 0 x,y и z такие что x(1,0,0) + y(0,1,0) + z(0,0,1) = (0,0,0). Если говорить более математически, то из любой пары векторов из этой тройки, можно получить плоскость, для которой 3-й вектор будет перпендикулярным (плоскость XY перпендикулярна оси Z, и т.д). Легко заметить, что система координат камеры задана векторами (1,0,-1), (0,1,0), (1,0,1). После нормирования векторы станут равны (0.7071,0,-0.7071), (0,1,0) и (0.7071,0,0.7071).
Следующее изображение показывает как вектор указывается в 2 независимых системах координат:
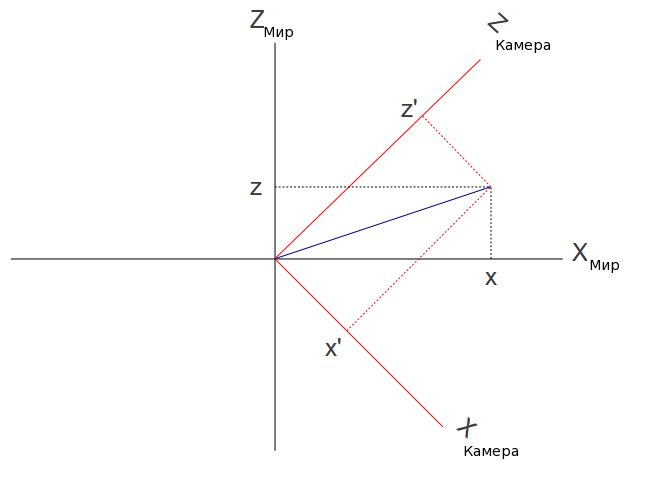
Мы знаем как получить единичные вектора, которые обозначат оси камеры в мировом пространства и мы знаем позицию вектора в нем (x,y,z). Нас же интересует вектор (x',y', z'). Теперь воспользуемся значением скалярного произведения, известного как 'скалярная проекция'. Скалярная проекция - это результат скалярного произведения между произвольным вектором A и единичного вектора B, и результат это величина A в направлении B. Другими словами, проекция вектора A на вектор B. В примере выше, если мы скалярно умножим вектор (x,y,z) и единичный вектор, представляющий X у камеры, то мы получим x'. Аналогично мы можем получить y' и z'. (x',y',z') это и есть координаты (x,y,z) в пространстве камеры.
Давайте рассмотрим как собрать из этих выводов единое решение для положения камеры. Решение называется 'UVN камера' и это одна из множества систем, характеризующих камеру. Идея в том, что камера определяется следующими векторами:
- N - Вектор от камеры к ее цели. Так же известен как вектор 'look at' в некоторой литературе о 3D. Этот вектор соответствует Z оси.
- V - Если стоять прямо, то этот вектор будет исходить из головы в небо. Если вы пишите симулятор полетов, и один из них перевернут, то вектор будет указывать на землю. Этот вектор соответствует оси Y.
- U - Этот вектор выходит из камеры направо. Соответствует оси X.
Итак, для перевода координат из мировой системы в систему камеры, определенную векторами UVN, нам необходимо найти скалярное произведение между вектором позиции с векторами UVN. Матрица лучше всего покажет как это происходит:
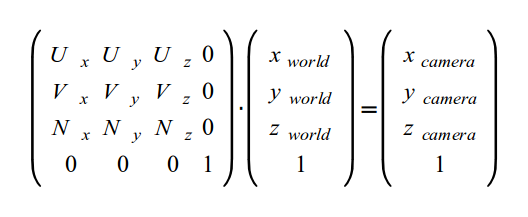
В исходном коде к этому уроку вы заметите, что переменная 'gWorld' теперь называется 'gWVP'. Это изменение отражает серии преобразований, известных во многих книгах. WVP расшифровывается как вид мировой проекции (World-View-Projection).
Прямиком к коду!
В этом уроке я решил сделать не большие изменения в структуре проекта и переместил низкоуровневые взаимодействия с матрицами из класса конвейера в их собственный класс. Теперь конвейер может инициализировать матрицу несколькими способами и собирает матрицы для создания итогового преобразования.
pipeline.h:85
struct {
Vector3f Pos;
Vector3f Target;
Vector3f Up;
} m_camera;
Класс конвейера имеет несколько новых параметров для хранения данных матрицы. Заметим, что у нас отсутствует вектор вправо. Он может быть подсчитан на ходу используя векторное произведение других векторов. Кроме того, появилась новая функция SetCamera для получения этих значений.
math3d.h:21
Vector3f Vector3f::Cross(const Vector3f& v) const
{
const float _x = y * v.z - z * v.y;
const float _y = z * v.x - x * v.z;
const float _z = x * v.y - y * v.x;
return Vector3f(_x, _y, _z);
}
Vector3f приобрел новый метод для векторного умножения между 2 векторами. Такая операция возвращает вектор, перпендикулярный плоскости, определяемой исходными векторами. Станет гораздо легче в понимании, когда вы вспомните, что вектор имеет направление и значения, но не имеет позиции. Все вектора, у которых совпадают направления и значения - эквивалентны, не зависимо от того, из какой точки они выходят. Поэтому вы можете представить, что все вектора выходят из начала координат. Это значит, что вы можете создать треугольник, одна из вершин которого начало координат, а 2 другие на конце векторов. Треугольник принадлежит плоскости, а результат векторного произведения дает вектор, перпендикулярный этой плоскости. Прочитайте подробнее о векторном произведении на Википедии.
math3d.h:30
Vector3f& Vector3f::Normalize()
{
const float Length = sqrtf(x * x + y * y + z * z);
x /= Length;
y /= Length;
z /= Length;
return *this;
}
Для генерации матрицы UVN мы должны сделать вектора единичной длины. Это называется 'нормировать вектор', заключается в том, что все компоненты вектора делятся на его длину. Подробнее об этом на Mathworld.
math3d.cpp:84
void Matrix4f::InitCameraTransform(const Vector3f& Target, const Vector3f& Up)
{
Vector3f N = Target;
N.Normalize();
Vector3f U = Up;
U.Normalize();
U = U.Cross(Target);
Vector3f V = N.Cross(U);
m[0][0] = U.x; m[0][1] = U.y; m[0][2] = U.z; m[0][3] = 0.0f;
m[1][0] = V.x; m[1][1] = V.y; m[1][2] = V.z; m[1][3] = 0.0f;
m[2][0] = N.x; m[2][1] = N.y; m[2][2] = N.z; m[2][3] = 0.0f;
m[3][0] = 0.0f;m[3][1] = 0.0f;m[3][2] = 0.0f;m[3][3] = 1.0f;
}
Эта функция генерирует преобразования камеры, которые позднее будут использованы конвейером. Векторы U,V и N высчитываются и заносятся в ряды матрицы. Так как вектор позиции будет умножаться справа (в виде столбца), то мы получим скалярное произведение между этим вектором и векторами U,V и N. Это вычислит значения 3 скалярных проекций, которые станут XYZ значениями позиции в пространстве экрана.
Функция получает вектор направления и верхний вектор. Вектор вправо вычисляется как их векторное произведение. Заметим, что мы хотим нормировать векторы в любом случае, даже если они уже единичной длины. После генерации вектор вверх пересчитывается как векторное произведение между векторами направления и вектором вправо. Причина станет ясна позднее, когда мы начнем двигать камеру. Проще обновить только вектор направления, но тогда угол между направлением и вектором вверх не будет равен 90 градусам, что нарушит линейность системы координат. После подсчета вектора вправо и затем векторно умножив его на вектор направления, мы получим обратно вектор вверх, тем самым мы получаем систему координат, у которой угол между любыми 2 осями равен 90 градусов.
pipeline.cpp:22
const Matrix4f* Pipeline::GetTrans()
{
Matrix4f ScaleTrans, RotateTrans,
TranslationTrans, CameraTranslationTrans,
CameraRotateTrans, PersProjTrans;
ScaleTrans.InitScaleTransform(m_scale.x, m_scale.y, m_scale.z);
RotateTrans.InitRotateTransform(m_rotateInfo.x, m_rotateInfo.y, m_rotateInfo.z);
TranslationTrans.InitTranslationTransform(m_worldPos.x, m_worldPos.y, m_worldPos.z);
CameraTranslationTrans.InitTranslationTransform(-m_camera.Pos.x, -m_camera.Pos.y, -m_camera.Pos.z);
CameraRotateTrans.InitCameraTransform(m_camera.Target, m_camera.Up);
PersProjTrans.InitPersProjTransform(m_persProj.FOV, m_persProj.Width,
m_persProj.Height, m_persProj.zNear, m_persProj.zFar);
m_transformation = PersProjTrans * CameraRotateTrans *
CameraTranslationTrans * TranslationTrans *
RotateTrans * ScaleTrans;
return &m_transformation;
}
Давайте обновим функцию, генерирующую итоговую матрицу преобразований объектов. Она станет немного сложнее с 2 новыми матрицами, характеризующими участие камеры. После завершения мировых преобразований (комбинация масштабирования, вращения и перемещения объекта), мы начинаем преобразования камеры 'движением' ее обратно в начало координат. Это делается смещением на обратный вектор позиции камеры. Поэтому если камера находится в точке (1,2,3), мы двигаем объекты на (-1,-2,-3). После этого мы генерируем вращение камеры, основываясь на направлении камеры и ее векторе вверх. На этом участие камеры завершено. В конце мы проецируем координаты.
main.cpp:76
Vector3f CameraPos(1.0f, 1.0f, -3.0f);
Vector3f CameraTarget(0.45f, 0.0f, 1.0f);
Vector3f CameraUp(0.0f, 1.0f, 0.0f);
p.SetCamera(CameraPos, CameraTarget, CameraUp);
Мы используем новый функционал в главном цикле рендера. Для размещения камеры мы движемся назад, вдоль отрицательного Z, затем сдвигаемся вправо и встаем прямо. Камера глядит вдоль возрастания оси Z и немного правее относительно начала координат. Вектор вверх для простоты положительный Y. Мы назначаем это в класс конвейера, а об остальном он позаботится сам.