Урок 07 - Вращение
Следующий на очереди трансформаций - это вращение, то есть, берется угол и точка, которую мы хотим вращать относительно оси. Для этого всегда будут меняться 2 координаты из 3 (X, Y и Z), а одна останется без изменений. Это значит, что путь будет лежать на одной из 3-х основных плоскостей: XY (когда вращение вокруг Z), YZ (повороты относительно X) и XZ (для Y оси). Можно подобрать преобразования для вращения вокруг произвольной оси, но они довольно сложные и пока что нам не нужны.
Давайте определим задачу в общих чертах. Сосредоточимся на следующей диаграмме:
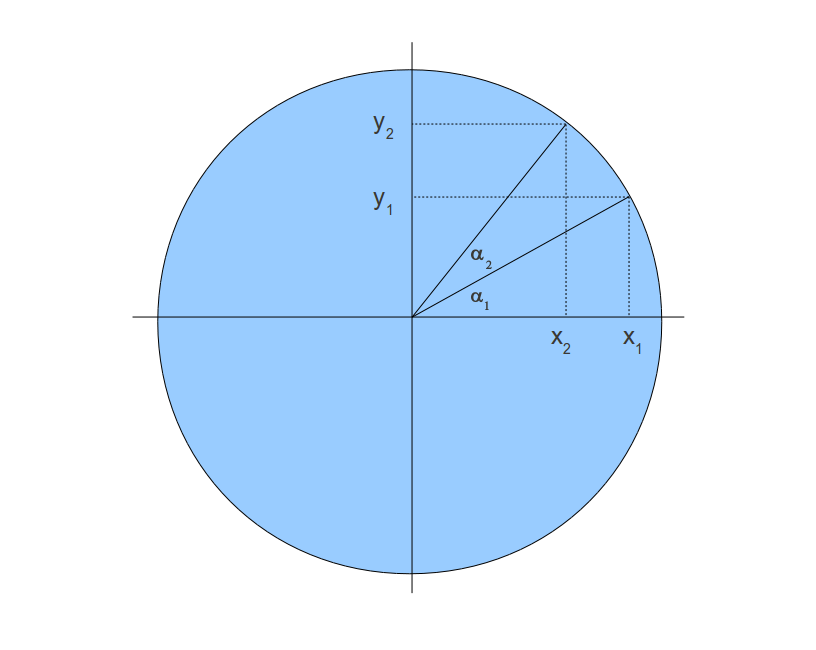
Мы хотим двигаться по окружности из (x1,y1) в (x2,y2). Другими словами, мы хотим повернуть точку (x1,y1) на угол a2. Предположим, что радиус окружности равен 1. Это означает следующее: x1=cos(a1) y1=sin(a1) x2=cos(a1+a2) y2=sin(a1+a2)
Мы будем использовать следующие тригонометрические тождества для нахождения x2 и y2: cos(a+b) = cosacosb - sina sinb sin(a+b) = sinacosb+cosa sinb
Используя формулы выше, можем написать: x2=cos(a1+a2) = cosa1cosa2 - sina1sina2 = x1cosa2 -y1sina2 y2=sin(a1+a2) = sina1cosa2 + cosa1sina2 = y1cosa2 + x1sina2
В диаграмме мы смотрим на плоскость XY, а ось Z - это точка. Если X&Y части 4-вектора, тогда уравнения выше можно записать в форме матрицы (не затрагивая Z&W):
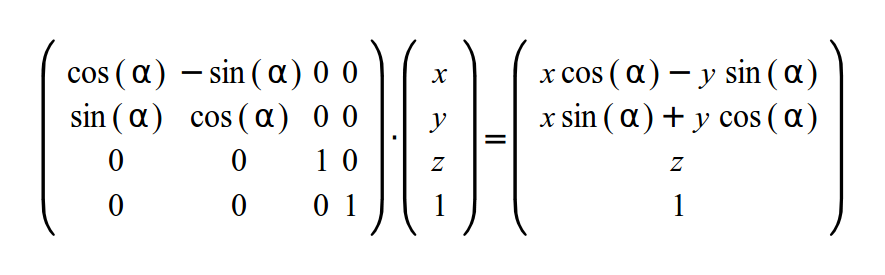
Если мы хотим задать вращение для Y и X осей, то выражения будут похожи, а вот матрицы устроены слегка по другому. Вот матрица для вращения вокруг Y оси:
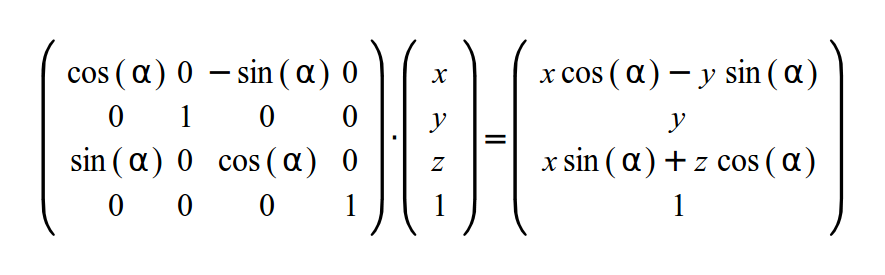
И матрица вращения вокруг X оси:
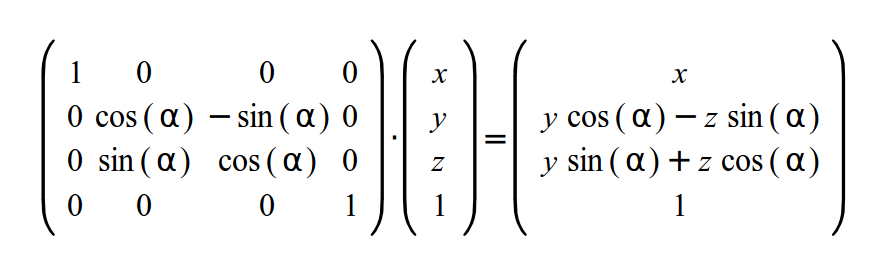
Прямиком к коду!
Изменения кода в этом уроке очень малы. Мы только изменяем значения единственной матрицы преобразований.
World.m[0][0]=cosf(Scale); World.m[0][1]=-sinf(Scale); World.m[0][2]=0.0f; World.m[0][3]=0.0f;
World.m[1][0]=sinf(Scale); World.m[1][1]=cosf(Scale); World.m[1][2]=0.0f; World.m[1][3]=0.0f;
World.m[2][0]=0.0f; World.m[2][1]=0.0f; World.m[2][2]=1.0f; World.m[2][3]=0.0f;
World.m[3][0]=0.0f; World.m[3][1]=0.0f; World.m[3][2]=0.0f; World.m[3][3]=1.0f;
Легко заметить, что мы задали вращение вокруг Z оси. Вы можете попробовать вращение вокруг других осей, но мне кажется, что без настоящей проекции из 3D в 2D другие типы вращения будут выглядеть немного странно. Мы их реализуем в классе полноценного конвейера в следующих уроках.