Урок 06 - Перемещение
В этом уроке мы начнем изучать различные преобразования для трехмерных объектов и их отображения на экран, создавая при этом иллюзию глубины сцены. Основной способ - это представление всех трансформаций в виде матриц, перемножая их одну за другой и затем умножая координаты вершин на итоговый результат. Каждый урок будет затрагивать по одному виду преобразований.
Сейчас мы будем рассматривать изменение координат, несущее за собой движение объекта вдоль вектора любой длины и направления. Скажем, что мы хотим передвинуть треугольник в левом изображении в такую же позицию, как и у треугольника справа:
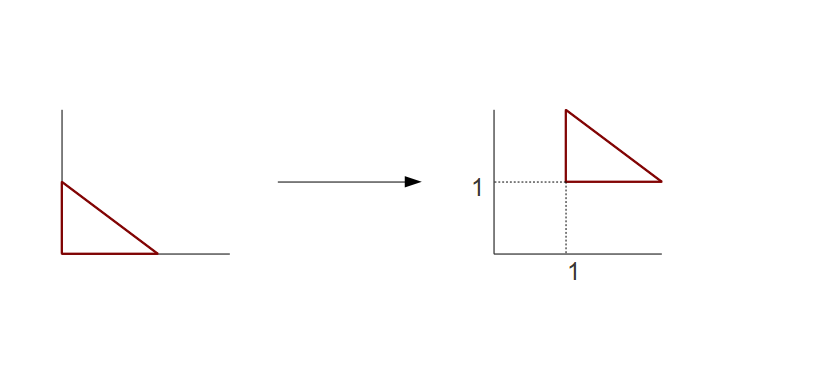
Один из способов это сделать - это создать вектор смещения (в нашем случае - 1,1) в виде uniform-переменной в шейдере и просто добавить его для каждой обрабатываемой вершины. Но это нарушает метод поочередного умножения группы матриц для получения единой комплексной трансформации. Кроме того, позже вы узнаете, что перемещение обычно не первая операция, поэтому вам придется умножать координаты на матрицу, задающую преобразование до перемещения, затем совершить смещение и затем умножить на матрицу для трансформаций, следующих за смещением. Это очень не удобно. Лучше найти матрицу, задающую перемещение и участвующую в перемножении всех матриц. Но вы можете подобрать матрицу, после умножения на которую нижняя левая точка (0,0) перешла бы в точку (1,1)? По правде говоря это не возможно, если использовать двухмерную матрицу (и даже с трехмерной для точки (0,0,0)). Итого имеем: нам нужна матрица M, которая имея точку P(x,y,z) и вектор V(v1,v2,v3) даст нам M * P=P1(x + v1, y + v2, z + v3). Проще говоря, это значит что матрица M перемещает точку P в позицию P+V. В P1 мы видим, что каждая координата это сумма соответствующих координат P и V. Левая сторона каждой суммы обеспечивается единичной матрицей: I * P = P(x,y,z). Похоже на то, что для начала мы берем единичную матрицу и теперь изучим, чего же нам не хватает в правой стороне каждой суммы координат (…+V1, …+V2, …+V3). Давайте посмотрим на немного улучшенную единичную матрицу:
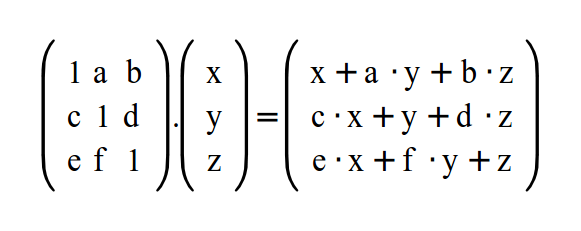
Из этих подсчетов можно сделать 2 вывода:
- a, b, c, d, e и f должны быть равны 0 иначе каждые 2 координаты будут влиять на третью (таким образом, мы вернулись к единичной матрице).
- Поскольку x, y и z влияют друг на друга, то в случае если они все будут равны 0, то и результат будет 0 (т.е мы не сможем перемещать нулевой вектор).
Мы же хотим найти матрицу, которая даст следующий результат в правой части:
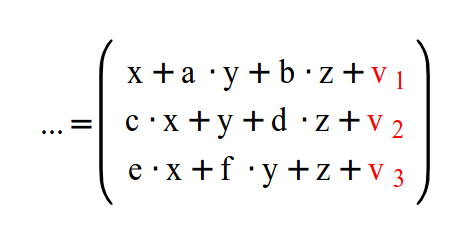
Нам нужно найти способ добавить v1-v3 как мы видим выше, а a-f равны 0. Итоговый результат - это наш вектор движения. Похоже на то, что нам необходимо добавить 4-й столбец в матрицу, но в этом случае нельзя будет производить наши подсчеты. Мы не можем умножать матрицу 3x4 на вектор 3x1. Правило гласит, что можно умножать матрицы, только если их размерности NxM и MxN. Тогда мы добавим 4-й элемент в вектор. Лучше взять его равным 1, тогда мы сможем поместить v1-v3 на четвертом столбце матрицы и они останутся без изменений в итоге, потому, что они будут умножены на 1. Но нашу матрицу по прежнему нельзя использовать для умножения, но если добавить 4-ю строку, матрица станет 4x4 и её уже можно умножать на наш вектор. Наконец, наше преобразование:
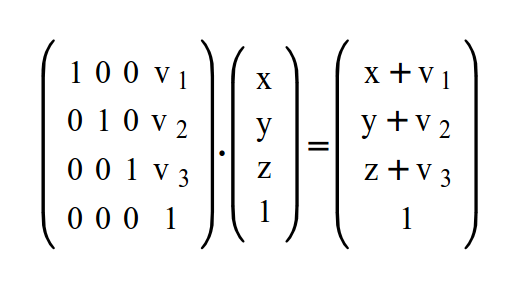
Теперь даже если x,y и z будут равны 0, мы все равно сможем их переместить в любую точку.
Первые 3 координаты вектора, как в случае сейчас, называются однородными координатами, такой подход очень популярен и полезен в 3D графике. Четвертый компонент называется 'w'. Фактически, внутренний символ шейдера gl_Position, который мы видели ранее, это 4х вектор и его w компонента играет очень важную роль для проектирования из 3D в 2D. В общем случае w=1 для точек и w=0 для векторов. Причина в том, что точки могут быть перемещены, а вот векторы - нет. Вы можете изменить длину или направление вектора, но вектора равны, если их направления/длина тоже равны, несмотря на их начальные позиции. Это можно использовать для всех векторов. Назначим w=0 и умножение матрицы сдвига на вектор всегда выдаст тот же самый вектор.
Прямиком к коду!
struct Matrix4f {
float m[4][4];
};
Мы создали структуру для матрицы 4 на 4 в файле math_3d.h. Начиная с этого момента она будет использоваться для большинства матриц преобразования.
GLuint gWorldLocation;
Мы используем этот указатель для доступа к всемирной матрице, представленной в виде uniform-переменной внутри шейдера. Всемирная она потому, что всё что мы делаем с объектом, это изменение его позиции в место, которое мы указываем относительно координатной системы внутри нашего виртуального 'мира'.
Matrix4f World;
World.m[0][0] = 1.0f; World.m[0][1] = 0.0f; World.m[0][2] = 0.0f; World.m[0][3] = sinf(Scale);
World.m[1][0] = 0.0f; World.m[1][1] = 1.0f; World.m[1][2] = 0.0f; World.m[1][3] = 0.0f;
World.m[2][0] = 0.0f; World.m[2][1] = 0.0f; World.m[2][2] = 1.0f; World.m[2][3] = 0.0f;
World.m[3][0] = 0.0f; World.m[3][1] = 0.0f; World.m[3][2] = 0.0f; World.m[3][3] = 1.0f;
В функции рендера мы подготавливаем матрицу 4x4 и заполняем в соответствии с объяснением выше. Мы устанавливаем v2 и v3 в 0, поэтому у объекта координаты Y и Z не будут изменяться, и мы записываем в v1 значения синуса. Это будет изменять координату X на значение, плавно переходящее от -1 и до 1. Теперь мы загрузим матрицу в шейдер.
glUniformMatrix4fv(gWorldLocation, 1, GL_TRUE, &World.m[0][0]);
Вот еще один пример функции glUniform* для загрузки данных в uniform-переменные шейдера. Здесь мы загружаем матрицу 4x4, так же есть версии для загрузки матриц размерностей 2x2, 3x3, 3x2, 2x4, 4x2, 3x4 и 4x3. Первый параметр - это адрес uniform-переменной (находится после компиляции шейдера используя glGetUniformLocation()). Второй параметр - это количество матриц, значения которых мы обновляем. Пока что мы указываем 1 для одной матрицы, но мы можем использовать эту функцию для обновления множество матриц в одном вызове. Третий параметр часто сбивает с толку новичков. Он указывает подается ли матрица по строковому или по столбиковому порядку. По строковая матрица означает, что матрица содержит строки одна за другой. По столбцам аналогично, но для столбцов. Дело в том, что языки C/C++ строковые по умолчанию. Это значит, что когда вы заполняете двумерный массив, то в памяти строки выстроены одна за другой, причем верхняя имеет наименьший адрес. Для примера рассмотрим следующий массив:
int a[2][3];
a[0][0] = 1;
a[0][1] = 2;
a[0][2] = 3;
a[1][0] = 4;
a[1][1] = 5;
a[1][2] = 6;
Визуально массив выглядит как следующая матрица: 1 2 3 4 5 6 В памяти эти слои выглядят так: 1 2 3 4 5 6 (у 1 наименьший адрес).
Наш третий параметр в glUniformMatrix4fv() - это GL_TRUE, потому что мы поставляем матрицу упорядоченную по строкам. Мы конечно же можем сделать третий параметр равным GL_FALSE, но тогда нужно транспонировать матрицу (в памяти программы на C/C++ значения располагаются по прежнему, но OpenGL будет "думать", что первые 4 значения, которые мы предоставляем, это столбец матрицы и будет вести себя далее соответственно). Четвертый параметр - это просто указатель на первый элемент матрицы.
Пройдемся по коду шейдера.
uniform mat4 gWorld;
Это uniform-переменная типа матрицы 4x4 . Так же доступны mat2 и mat3.
gl_Position = gWorld * vec4(Position, 1.0);
Позиции вершин треугольника в буфере вершин - это вектор 3 элементов, но мы уже решили, что необходим 4-й компонент, равный 1. Есть 2 решения: можно добавлять 4 компонент в вершинный буфер или сразу в вершинный шейдер. У первого нет никаких преимуществ: каждая вершина будет тратить дополнительные 4 байта памяти для компонента, который и так известно, что будет равен 1. Более эффективно остаться с вектором в 3 компонента и привязывать w компонент в шейдере. В GLSL для этого используем 'vec4(Position, 1.0)'. Мы умножаем матрицу на вектор и результат передаем в gl_Position. Подводя итог, в каждом кадре мы генерируем преобразование матрицы, которое изменяет X координату на величину, которая меняется между -1 и 1. Шейдер умножает позицию каждой вершины на матрицу, в результате объект движется то влево, то вправо. В большинстве случаев одна из сторон треугольника выходит из экрана после действия шейдера, и тогда клипер обрезает эту сторону. Мы сможем увидеть только оставшуюся часть.